非线性回归的基本思想

如果不先掌握矩阵代数，就无法理解非线性回归的数学细节。但基本思想还是很容易理解的。每种非线性回归方法都遵循以下步骤：

1.从方程中每个参数的初始估计值开始。

2.生成由初始值定义的曲线。计算平方和--各点与曲线垂直距离的平方和。(如果包含加权因子，则计算加权平方和）。

3.调整参数，使曲线更接近数据点 - 减少平方和。如下所述，有几种调整参数的算法。

4.4. 再次调整参数，使曲线更接近数据点。重复。

5.当调整对平方和几乎没有影响时，停止计算。

6.报告拟合优度结果。获得的精确值部分依赖于步骤 1 中选择的初始值和步骤 5 中的停止标准。这意味着重复分析相同的数据并不总能得到完全相同的结果。

马夸特方法

第 3 步是唯一困难的一步。Prism （和大多数其他非线性回归程序）使用的是 Marquardt 和 Levenberg 方法，它融合了另外两种方法，即线性下降法和高斯-牛顿法。了解这些方法的最好方法是按照本示例进行操作。下面是一些要拟合成典型结合曲线（直角双曲线）的数据。

 

 

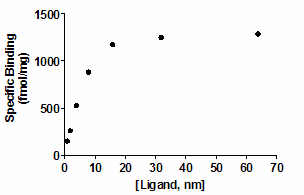
您想拟合一条结合曲线来确定 Bmax 和 Kd，公式为

 

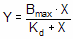
如何找到拟合数据最优度的 Bmax 和 Kd 值？您可以通过改变 Bmax 和 Kd 生成无数条曲线。对于生成的每条曲线，您都可以计算平方和，以评估该曲线与数据的拟合程度。下图说明了这种情况。

 

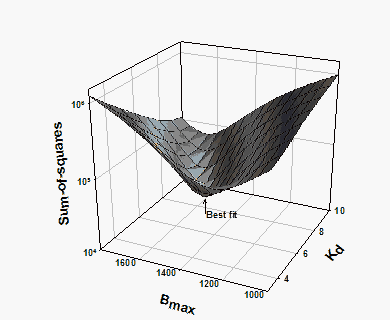
X 轴和 Y 轴分别对应于非线性回归拟合的两个参数（本示例中为 Bmax 和 Kd）。Z 轴是平方和。曲面上的每个点对应一条可能的曲线。非线性回归的目标是找到 Bmax 和 Kd 的值，使平方和尽可能小（找到谷底）。

线性下降法遵循一种非常简单的策略。从初始值开始，尝试少量增加每个参数。如果平方和下降，则继续。如果平方和上升，则返回并减少参数值。这样就向下移动了一步。重复多次。每一步通常都会降低平方和。如果平方和反而上升了，那一定是步子迈得太大，以至于你越过了底部，又从另一侧回到了底部。如果出现这种情况，请返回并迈出较小的一步。多次重复这些步骤后，就会到达底部。

高斯-牛顿法比较难理解。与线性下降法一样，首先要计算当你对每个参数的值做微小改变时，平方和会发生多大变化。这将告诉你平方和曲面在初始值所定义的点上的斜率。如果方程确实是线性的，那么这些信息就足以确定整个平方和曲面的形状，从而一步计算出 Bmax 和 Kd 的拟合优度值。对于线性方程，只要知道一点的斜率，就可以知道关于曲面的所有信息，从而一步就能找到最小值。对于非线性方程，高斯-牛顿法不会一步就找到拟合优度值，但这一步通常会改善拟合效果。在重复多次迭代后，就会达到最小值。

这种线性下降法在早期迭代时往往效果很好，但在接近拟合优度值（曲面接近平坦）时，效果就会很慢。相比之下，高斯-牛顿法在早期迭代时往往效果不佳，但在后期迭代时效果很好。这两种方法在马夸特方法（又称莱文伯格-马夸特方法）中得到了融合。它在早期迭代中使用线性下降法，然后逐渐切换到高斯-牛顿法。

Prism 和大多数程序一样，使用马夸特方法进行非线性回归。该方法非常标准。唯一的变化是使用什么值的 lambda（决定步长），以及如何随连续迭代改变 lambda。我们遵循 Numerical Recipes 的建议。Lambda 初始化为 0.001。迭代成功后，它将减少 10 倍；迭代失败后，它将增加 10 倍。

参考文献                                                                           

第 15 章 Numerical Recipes in C, Second Edition, WH Press, et.剑桥出版社，1992 年

SA Glantz 和 BK Slinker 合著的《 应用回归和方差分析入门》第 10 章  ，McGraw-Hill，1990 年。