引言

在标准 单相衰减 方程 中  ，衰减从时间 0 开始。 当您测量一段时间的基线，然后进行一些实验干预，使衰减从某个时间 X0 开始时，就会用到这个方程。

输入数据

创建 XY 数据表。在 X 列中输入时间，在 Y 列中输入响应（结合力、浓度......）。如果有多个实验条件，则将第一个条件放入 A 列，第二个条件放入 B 列，等等。

输入数据后，单击 "分析"，选择非线性回归，选择指数方程面板，然后选择 "高原 "和 "单相衰减"。

考虑将 X0 和 Plateau 限制为一个常数值

如果您知道初始衰减值的时间，则应将 X0 限制为该值。

在这种情况下，应将参数 Plateau 限制为等于零的恒定值。

要将参数限制为常数，请转到非线性回归对话框的 "限制"选项卡，将参数名称旁边的下拉菜单设为 "常数等于"，然后输入数值。

模型

Y= IF( X<X0, Y0, Plateau+(Y0-Plateau)*exp(-K*(X-X0)))

 

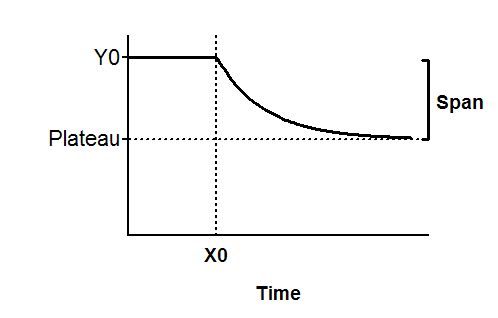
X0 是衰减开始的时间。通常情况下，您会根据实验设计将其设置为一个恒定值，但 Prism 也可以拟合它。它的时间单位与 X 相同。

Y0是截至时间 X0 的平均 Y 值。其单位与 Y 相同、

Plateau是无限时间的 Y 值，单位与 Y 相同。

K是速率常数，用 X 轴时间单位的倒数表示。如果 X 以分钟为单位，则 K 以倒数分钟为单位。

Tau是时间常数，单位与 X 轴相同。它是以 K 的倒数来计算的。

半衰期以 X 轴的时间单位表示。计算公式为 ln(2)/K。

跨度是 Y0 和高原之间的差值，单位与 Y 值相同。