引言

除非能根据其他实验将koff约束为一个恒定值，否则无法通过在单一浓度放射性配体下测得的结合率来确定kon。观测到的结合速率依赖于结合速率常数、配体用量及其解离速率常数。使用一种浓度的放射性配体，结果是模糊的。.

如果使用多种放射性配体浓度进行关联动力学实验，可以将数据与关联动力学模型进行全局拟合，得出kon和koff 的单一最佳拟合优度估计值。

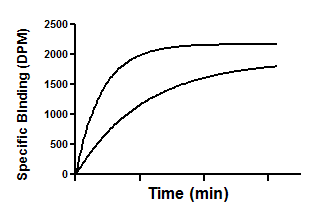
下图是使用两种浓度放射性配体进行关联动力学实验的本示例。当然，两次实验的所有其他条件（温度、pH 值等）均相同。时间输入 X 列，一种浓度放射性配体的特异性结合输入第一（A）Y 列，另一种浓度的结合输入 B 列。

步骤

创建 XY 数据表。在 X 列输入以分钟为单位的时间，在 Y 列输入总结合。在 A 列输入一种浓度放射性配体的结合情况，在 B 列输入另一种浓度的结合情况，等等。在列标题中输入浓度（以 nM 为单位）。

在特异性结合表中单击 "分析"（Analyze），选择 "非线性回归"（nonlinear regression），选择 "动力学结合方程"（Kinetics Binding equations）面板，然后选择 "关联--两种或两种以上浓度的热"（ Association-Two or More conc.）

模型

Kd=Koff/Kon

L=Hotnm*1e-9

Kob=Kon*L+Koff

占有率=L/（L+Kd）

Ymax= 占用率*Bmax

Y=Ymax*(1 - exp(-1*kob*X))

解读参数

Koff是解离速率常数，单位为 min-1。

Kon是结合速率常数，单位为 M-1 min-1。

Kd是平衡解离常数，单位为摩尔，计算公式为 Koff/Kon

Bmax是最大放射性配体浓度下的平衡时最大结合量，单位为 Y。

注释

根据质量作用定律，Koff 与 Kon 之比就是受体结合的 Kd：

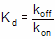
将这种方法（通过动力学实验）计算出的 Kd 与饱和结合曲线确定的 Kd 进行比较。如果结合遵循质量作用定律，那么这两个 Kd 值应该是没有区别的。