引言

如果酶具有合作亚基，则酶的速度与底物浓度的函数关系图将呈现半正态分布。Prism 提供了一个拟合底物-速度曲线的经验公式。请阅读有关酶动力学的高级书籍，了解基于别构作用分子模型的其他方法。

如何输入数据

创建 XY 数据表。在 X 列中输入底物浓度，在 Y 列中输入酶的速度。如果有多个实验条件，则将第一个条件放入 A 列，第二个条件放入 B 列，等等。

输入数据后，点击分析，选择非线性回归，选择酶动力学方程面板，然后选择变构 S 形酶动力学。

模型

Y=Vmax*X^h/(Khalf^h + X^h)

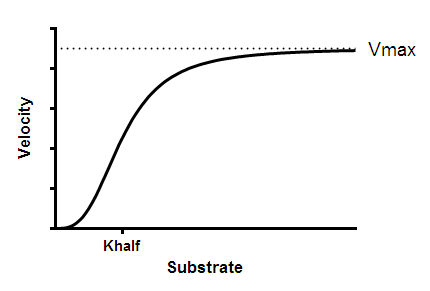
解读参数

Vmax是酶的最大速度，单位与 Y 相同。它是推断出底物浓度非常高时酶的速度，因此几乎总是高于实验中测得的任何速度。

Khalf是产生半最大酶速的底物浓度。它就是 EC50。

h是 Hill 斜率。当 h=1 时，该方程与标准Michaelis-Menten 方程相同。当 h 大于 1.0 时，由于正向协同作用，曲线呈曲线形。变异性 h 并不总是等于相互作用结合位点的数量，但其值不能超过相互作用位点的数量。可以把 h 看作是曲线陡峭程度和合作性存在与否的经验度量。

Kprime与 Km 有关。其计算公式为 Khalf^h，单位与 X 相同。

方程的另一种形式

该方程的另一个版本（下文引用的科普兰博士著作中的方程 5.47）与 Kprime 相符。

Y=Vmax*X^h/(Kprime + X^h)

请注意，该方程中的 Kprime 等于 Prism 内置方程中的 Khalf^h。这两个模型生成的曲线完全相同，只是报告参数的方法不同而已。Prism 同时报告 Kprime 和 Khalf。

参考                                                                        

方程式 5.47，载于 RA Copeland，《 酶》， 第 2 版，Wiley，2000 年。在该参考文献中，Copeland 演示了如何拟合 Kprime。通过个人交流，他扩展了该模型以同时拟合 Khalf。