什么是假最小值？

非线性回归程序会对变量进行小步调整，以提高拟合优度。如果 Prism 收敛到一个答案上，那么可以肯定，稍微改变任何变量都会使拟合效果变差。但从理论上讲，变量的较大变化可能会导致拟合优度大大提高。因此，Prism 得出的 "最佳"曲线可能并非最佳。

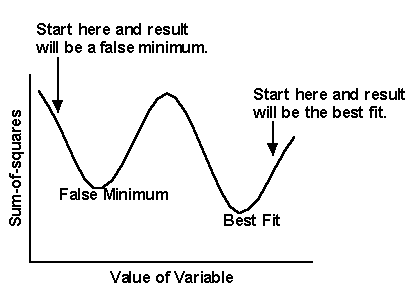
将纬度和经度视为 Prism 试图拟合的两个变量。现在将海拔高度视为平方和。非线性回归通过迭代来减少平方和。这就像走下坡路寻找谷底一样。当非线性回归收敛后，改变任何变量都会增加平方和。当你在谷底时，每个方向都是上坡。但是，在山脊上可能还有一个更深的山谷，而你却不知道。在非线性回归中，变量的较大变异性可能会降低平方和。

无论使用什么程序，这个问题（称为寻找局部最小值）都是非线性回归的固有问题。如果数据散布较少，在适当的 X 值范围内收集数据，并选择了适当的方程，就很少会遇到局部最小值。

测试错误最小值

测试是否存在假最小值：

1.注意变量值和第一次拟合的平方和。

2.对一个或多个参数的初始值进行较大改动，然后再次运行拟合值。

3.重复步骤 2 多次。

理想情况下，无论初始值如何，Prism 都会报告几乎相同的平方和和参数。如果数值不同，则接受平方和最小的参数。