用方差多重比较检验来比较每个剂量的两条剂量反应曲线(或每个时间点的两条时间历程曲线)有意义吗?
没有意义。
可以使用双向方差分析来比较两条剂量反应曲线或时间历程曲线。这种方法的问题在于,单向方差分析对待不同剂量(或时间点)的方式与对待不同物种或不同药物的方式相同。方差分析忽略了不同剂量(或时间)的顺序或数字这一事实。您可以随意改变剂量或时间,但仍然可以得到相同的方差分析结果。
如果没有足够的数据或理论来拟合曲线,方差分析可能是比较曲线的第一步。你会得到一个检验所有剂量导致相同效果的零假设的 P 值,另一个检验所有(两种)处理无差别的零假设的 P 值,第三个检验是否存在交互作用--处理之间的差异在所有剂量下是否一致。第一个 P 值总是很小,而且信息量不大(治疗当然有作用)。第二个 P 值可能是您最关心的,因为它询问的是两条曲线之间的差异。
然后在每个剂量(或每个时间点)进行多重比较检验,询问治疗组之间的差异在统计学上是否显著,这很有诱惑力。我不明白这些多重比较检验如何提供有用的信息。如果你有两条截然不同的剂量反应曲线,你就会期望在低剂量时看到微小的差异,而在中间剂量时看到较大的差异。在每个剂量下进行多重比较检验有助于你了解你的系统吗? 它能帮助你设计出更好的实验吗?我认为这两个问题的答案几乎总是否定的。
有什么办法呢?使用非线性回归来提出一个有针对性的问题。在本例中,使用非线性回归来量化 EC50 的折移及其置信区间,并计算检验无折移这一零假设的 P 值。详情请点击此处。
问产生统计学显著差异的最低剂量是多少是否有意义?
没有意义。
有些人想把注意力集中在低剂量上,他们会问:在两种治疗方法之间产生统计学显著差异的最低剂量是多少?"显着"一词往往会影响清晰的思路,因此,我们不妨把这个问题翻译成:"数据显示,产生显着差异的最低剂量是多少?最低剂量是多少,数据能让我相信两条曲线之间的差异是治疗造成的,而非偶然?" 答案部分依赖于你在每个剂量下重复多少次。你可以通过增加重复次数来降低最低显效剂量。我看不出这对你更好地理解你的系统有什么帮助,也看不出这对你设计更好的实验有什么帮助。
下面的模拟数据证明了这一点。两幅图都是使用四参数变异性斜率剂量反应曲线模拟的,参数和随机变异性的数量相同。左边的图表每个剂量有三个数据点(三重复)。右图每个剂量有 24 个重复点。
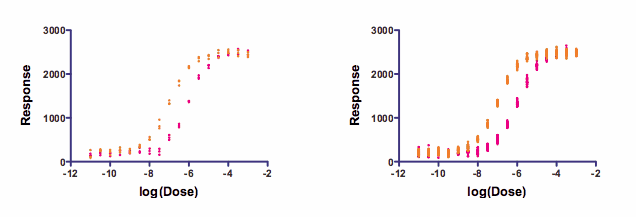
数据采用双向方差分析和 Bonferroni 多重比较检验进行分析。
对于左侧的图表,当对数(浓度)为-8 时,两个数据集之间的差异首次出现统计学显著性(使用 Bonferroni 对比较族应用 alpha =0.05)。
而右图中,当对数(浓度)为-9 时,差异首次出现统计学显著性。介于这两个值之间的浓度(1nM 到 10nM)会对右图产生统计学显著影响,但不会对左图产生影响。
我进行了多次模拟,结果是一致的,因此这不仅仅是随机数的怪异。相反,它证明了使用更多的重复样本可以将较小的差异检测为 "统计学显著"。
通过改变实验设计,我们可以改变问题的答案:两种药物的反应在统计学上有差异的最低浓度是多少?这说明这个问题不值得一问。