在对话框的选项选项卡中，您需要做出两个重大决定，它们会对 PCA 的结果和结论产生重 大影响。除非您明白为什么要另做决定，否则我们建议您在标准化数据上执行 PCA，并使用平行分析法选择成分数。

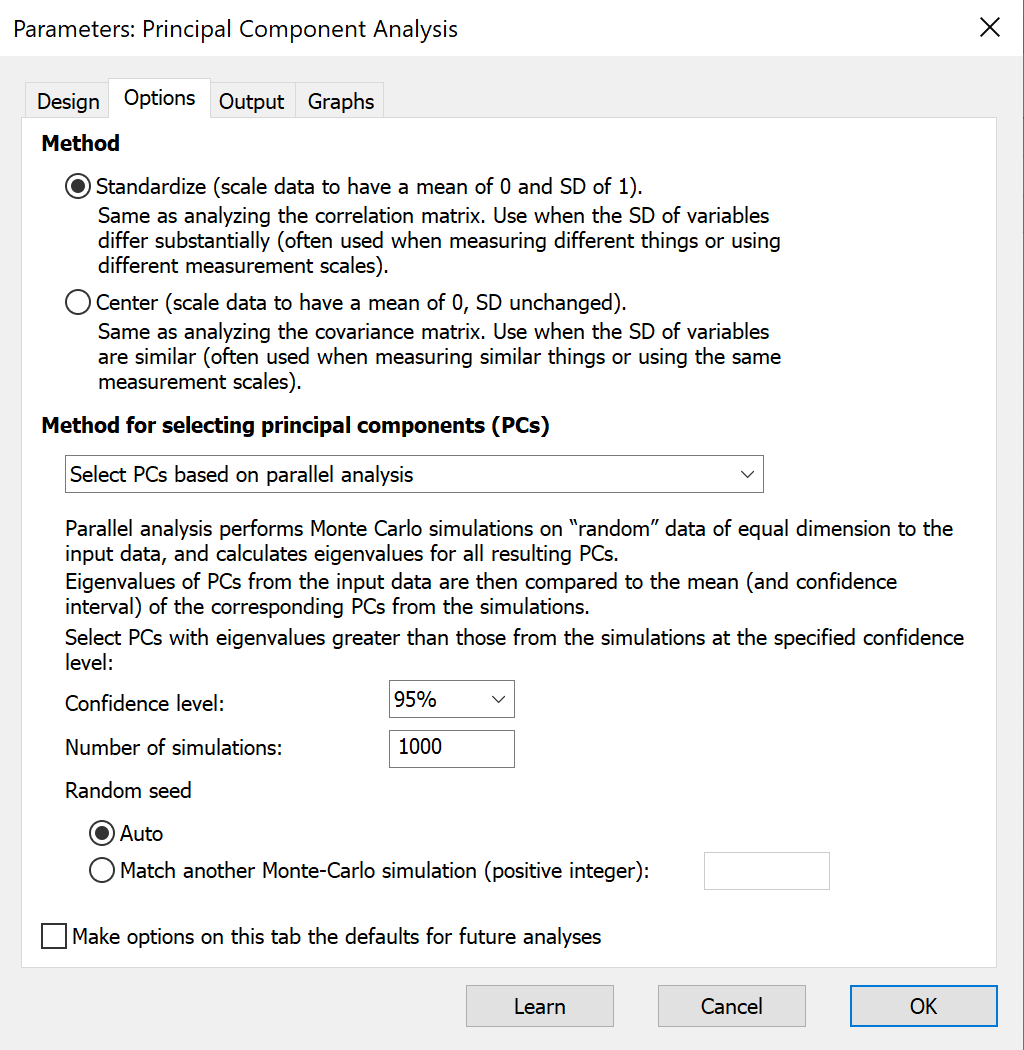
方法

最重要的决定是在标准化数据还是居中数据上执行 PCA。

在标准化数据上执行 PCA

除非有特异性原因，否则建议采用这种方法。有时也称为在相关矩阵上执行 PCA。如果您的变量使用不同的单位测量，您几乎总是会选择这种方法。

工作原理在进行 PCA 之前，先对变量进行变异性处理，使每个变量的平均值为 0，标准偏差为 1。这样，所有变量都处于同一量级上，在找到 PCs 时，每个变量的权重都相同。在数学上

标准化 X = (Xraw - X̄)/sx

其中，X̄ 是平均值，sx 是变量值的标准偏差。

居中数据的 PCA

如果所有变量的单位都相同，则可能需要对居中数据执行 PCA，也称为协方差矩阵 PCA。有时这也是合适的选择，但并不多见。

工作原理在执行 PCA 之前，要对变量进行变异性处理，使每个变量的均值为 0，标准偏差不变。由于变量没有标度，标准偏差比其他变量大的变量将主要驱动第一个主成分的计算。数学上

Xcentered = (Xraw - X̄)

其中，X̄ 是变量值的平均值。

选择主成分个数的方法

选择主成分是决定 PCA 后降维数据集 "维数"多少的过程。在某些情况下，Prism只提供所选 PC 的结果（载荷、特征向量、变量贡献矩阵、变量与 PC 的相关矩阵、PC 分数和案例贡献矩阵）。

Prism 提供了四种选择主成分数量的方法：

平行分析法（推荐）

平行分析是一种优雅的模拟程序，通过确定 PC 与模拟噪声产生的 PC 之间的差异点来选择要包含的 PC 个数。以下是并行分析的工作过程：

1.Prism 模拟大量数据集（默认为 1000 个，也可指定不同的数据集）。每个模拟数据集包含与输入数据相同数量的变量（列）和观测值（行）。

a.对于每个模拟变量，数据都是从均值为 0 的多维正态分布中采样生成的。

b.每个模拟变量的标准偏差等于输入数据表中相应变量的标准偏差。

2.对每个模拟数据集进行 PCA 计算

3.对于每个 PC，计算所有模拟数据集的平均特征值

4.对于每个 PC，使用所有模拟数据集的特征值计算上百分位数（默认为第 95 百分位数

5.对于每个 PC，Prism 会将输入数据的特征值与模拟数据集计算出的上百分位数进行比较

6.如果输入数据的特征值大于模拟数据的上百分位数，则选择该成分，否则不选择该成分。

请注意，如果您选择平行分析来确定 PC 的数量，则树状图将显示模拟特征值和数据特征值。

根据特征值选择 PC

通常情况下，选择特征值大于 1 的 PC。这就是所谓的凯泽规则。使用 "1"作为分界线的原因是，在标准化数据中，每个变量的标准偏差（和变异性）都等于 1。PC 的特征值代表 PC 与原始数据之间的方差。因此，如果每个原始变量（或列）引入的变异性为 1，则特征值小于 1 的 PC 解释的变异性小于单列数据。

Prism 还提供了一些选项，可选择不同的截止值或只保留特征值最大的前 k 个 PC（可在选项中指定 k）。

根据总解释方差的百分比选择 PCs

选择 PC 个数的另一种常见（经典）方法是保留具有最大特征值且累计解释了指定百分比总 方差的 PC。常用的目标总方差百分比为 75% 和 80%。

选择所有 PC

最后一个选项是让 Prism 报告所有 PC。这很少有用，但对于教学或特殊数据探索可能有用。