实验设计

您测量了对照组和治疗组大鼠的一个变异性。每组有三只大鼠，您对每只大鼠进行了四次技术重复测量。 请注意，每个子列中堆叠的四个值的顺序是任意的。这四行的顺序没有时间过程或任何其他含义。

 

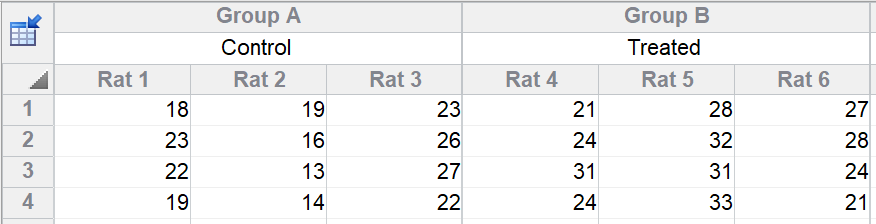
为什么要嵌套？

之所以说这个设计是嵌套的，是因为每只大鼠要么是对照组，要么是治疗组。您不能问是否有些大鼠对治疗的响应者比其他大鼠更好，因为每只大鼠只接受了其中一种替代治疗。大鼠被称为治疗内嵌套。

这也叫做分层设计。分层和嵌套是描述这种设计的同义词。

不正确的分析：对所有数据进行 t 检验

将这些数据视为每组 n=12 很有诱惑力，但并不恰当。

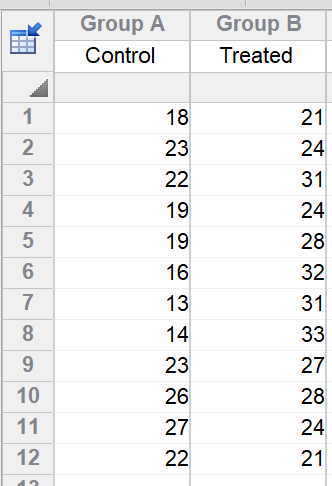
如果对这些数据进行 t 检验，均值差异的 95% 置信区间为 3.2 到 10.5，检验从均值相同的群体中抽样的单侧置信区间的零假设的 P 值为 0.0008。这似乎是治疗增加了结果变异性的有力证据。但这些结果并没有意义。

为什么没有意义？因为 t 检验值假定每个值都提供了独立的信息。这些数据中，每种治疗方法都有三只独立的大鼠，但却没有十二个独立的结果测量值。每只动物的重复值彼此接近，而不是从其他动物身上获得的值彼此接近。另一种说法是，当你把三只重复大鼠和每只大鼠内的四个技术重复结合起来时，得到的 12 个值就是伪重复。把伪重复当作实际重复来分析，会得到一个太窄的置信区间和一个太小的 P 值。

不正确的分析：双向方差分析

本页顶部显示的数据集似乎是为双向方差分析设置的。 但运行双向方差分析会导致不正确或误导性的结果。双向方差分析会假定第 2 行中数据的那类大鼠以某种方式暴露于控制数据和处理条件下。但事实上，每个子列中的值的顺序是任意的，因此在双向方差分析中将行作为一个 "因素"来检验是没有意义的。

无嵌套 t 检验的替代分析（仅在样本量相等时有效）

如果没有缺失值，可以用 t 检验来分析数据。第一步是平均每只大鼠的技术重复数据。然后将这些平均值输入新的表格，再用非配对 t 检验比较两组平均值。请注意，在进行 t 检验时，每组中的三只大鼠是叠加在一列的，而在嵌套 t 检验时则是并列在子列的。

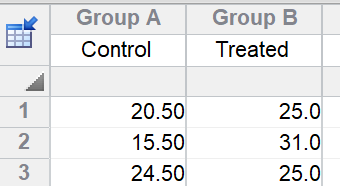
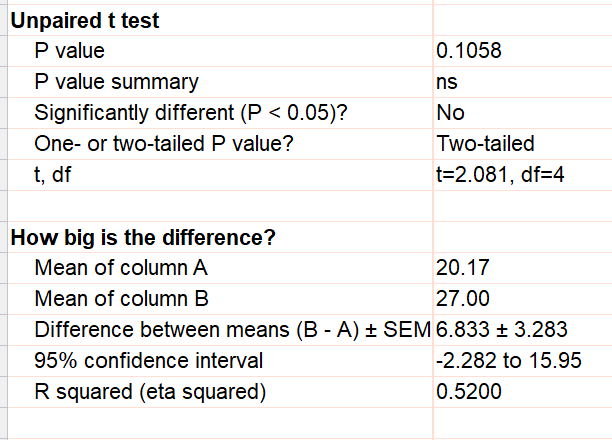
只要没有缺失值，就能得到正确的结果。有了这个正确的结果，差异的 95% 置信区间为-2.3 到 15.9，P 值为 0.1058。请注意，这里的结论（没有治疗效果的证据）与您通过分析伪重复得出的错误结论大相径庭。

Prism 中的嵌套 t 检验

Prism 8 引入了一种新的分析方法--嵌套 t 检验，可以一步完成分析并处理缺失值。它假定子列均值是从子列均值的高斯群体中采样的，而子列中的重复样本是从高斯群体中采样的。这两个高斯群体通常会有不同的标准偏差，Prism 会计算（估计）这两个标准偏差，并将其报告为 SD 和方差。