为了演示Kaplan-Meier 生存分析中使用的计算方法是如何工作的，请考虑以下生存数据：

该数据表示了一项包含 20 名参与者的研究、每位参与者的随访时间，以及每位参与者是否经历了感兴趣的事件或是否被删剪（这与讨论删剪的章节中用于生成可视化的数据相同）。

使用Kaplan-Meier 方法手动生成生存曲线的第一步是按经过时间升序对数据进行排序（Prism 会在 "幕后"为您完成这项工作，因此在 Prism 中执行Kaplan-Meier 分析时无需这样准备数据）。下表显示了重新整理后的数据：

既然数据已经得到了适当的排列，那么就可以使用Kaplan-Meier 方法来估算事件发生时每个时间点的存活概率。要手动完成这项工作，我们需要确定每个时间点的一些信息，包括

•时间 t 的风险人数 (Nt)

•时间点的事件数 (Et)

•时间 t 的删剪观测值数量 (Ct)

在个体还没有经过任何时间之前（时间 = 0），我们总共有 20 名参与者（假定都处于 "风险中"），并且在时间为零时没有死亡或删剪观测值。因此，0 时的存活概率为 1（或 100%）。

接下来，我们为我们掌握信息的每个经过时间添加一行。需要注意的是，在时间 t 发生事件或被删剪的个体在时间 t 仍被视为处于风险中。然而，由于我们知道他们经历了事件或被删剪，因此他们不再包含在任何后续时间点的风险人数中。让我们先在表格中增加一行：

观察原始数据，我们发现在经过时间 = 1 时，有一个事件（参与者 03）和一个删剪观测值（参与者 08）。利用这些信息，我们可以用下面的公式计算出这一经过时间的生存概率：

利用上表中的数字，我们可以计算出生存概率为：

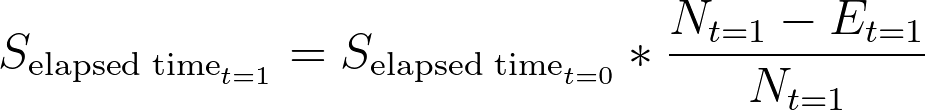
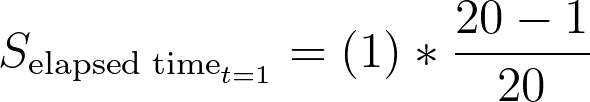
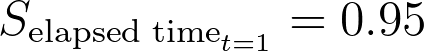
这意味着在该人群中，估计一个月后的存活概率（未发生相关事件的概率）为 95%。请注意，在计算存活概率时不会用到删剪观测值的数量（Ct）（因为我们不知道这些人何时真正经历了该事件）。但是，在计算下一个时间点的风险人数时会用到。也许大家都很清楚，为什么在某一特定时间经历了该事件的个体在之后的时间不会被纳入 "高危 "人群（他们已经经历了该事件）。当一个观察结果在某一给定时间被删剪时，意味着这是对该个体的最后一次观察，他们还没有经历过该事件。但是，由于我们不知道此人何时会经历该事件，因此无法将其纳入研究后期的风险人数中。因此，计算给定时间（Nt）的风险人数的一般公式等于前一时间的风险人数（Nt-1）减去前一时间的事件数和删剪观察数。在经过时间 t = 1 时，我们有 Nt = 20、一个事件和一个观测值。这意味着在下一个经过时间点（t = 2），我们将有 20 - 1 - 1 = 18 个风险点。下面的表格为下一个时间点添加了新的一行：

如前所述，存活概率的计算公式为

 

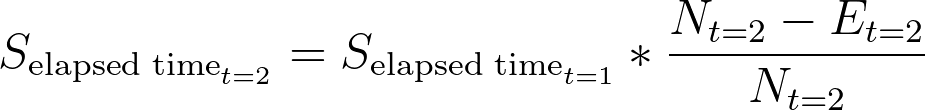
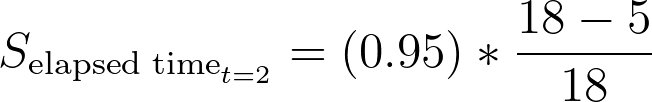
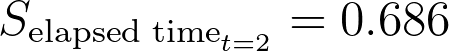
如前所述，这意味着该人群两个月后的估计存活概率约为 69%。表格的其余部分也可以用类似方法完成：

利用上表中的 "经过时间"和 "生存概率"值，可以绘制出如下所示的阶梯式生存曲线：

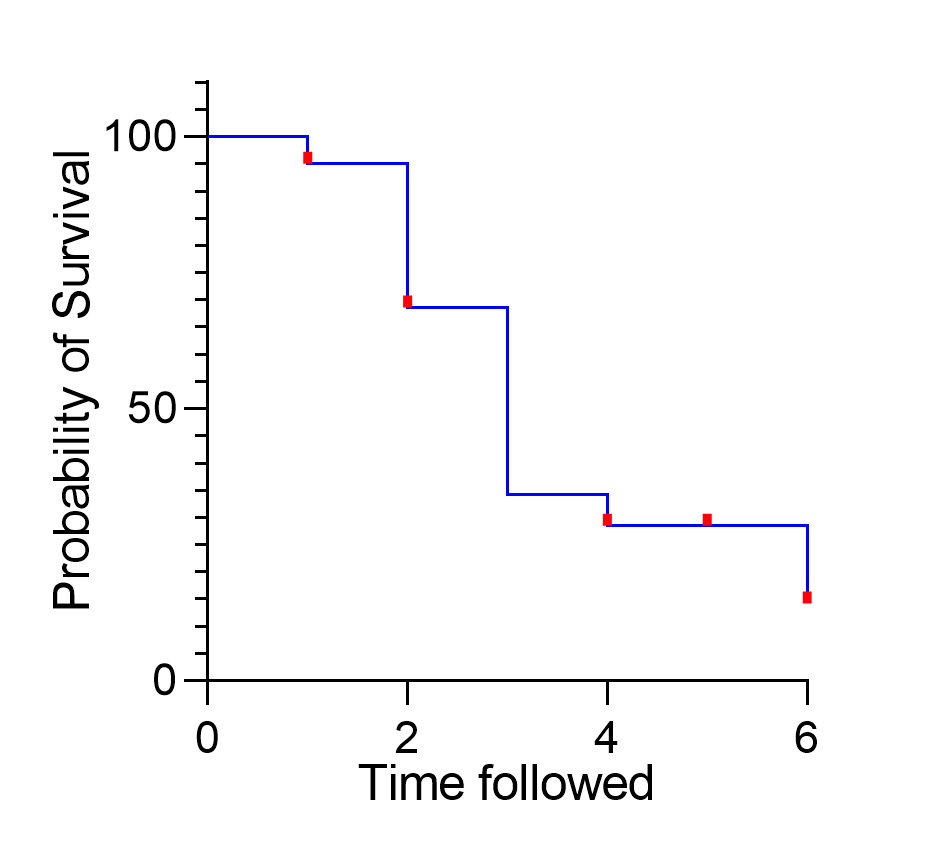
前面提到过，在计算生存概率的公式中并没有（直接）使用删剪观测值，但在确定下一个时间点的风险人数时会用到。从表中可以看出这一点，看计算出的经过时间 4 和 5 的生存概率，再看图形上时间跟随=5 时的曲线。在图上，红色的勾表示在这个时间点有观测值被删剪，但因为曲线没有垂直下降，所以显然在这个时间点没有事件发生。同样，在表格中，由于第 5 个时间点的事件数（Et）为零，因此计算出的生存概率在该时间点与紧随其后的时间点之间没有变化。

在 Prism 中执行此类分析非常简单，Prism 会自动计算并报告所有这些值以及估计生存概率图。本指南的这一部分详细介绍了如何使用 Prism 进行这种分析。