McNemar 检验概览

在通常的病例对照研究中，研究者将一组对照组与一组病例进行比较。作为一个对照组，对照组应该与病例相似（除了没有疾病）。进行病例对照研究的另一种方法是根据年龄、性别、职业、地点和其他相关变异性，将个别病例与个别对照进行匹配。麦克尼玛检验就是为这种研究设计的。

在普通的列联表上显示和分析配对病例对照研究的数据，会掩盖病例和对照是配对的这一事实。匹配使实验更有说服力，因此分析时应考虑到这一点。

本示例

下面是一些样本数据：

研究人员研究了 134 个病例和 134 个匹配的对照组，共计 268 个受试者。表中的每个条目代表一对（一个病例和一个对照）。"+"和"-"标签指的是暴露于或未暴露于推测的风险因素或暴露的人群。

这不是一个列联表，因此通常的列联表分析不会有帮助。事实证明，优势比的计算非常简单。13 对病例和对照组都暴露于风险因素的情况没有提供风险因素与疾病之间关联的信息。同样，病例和对照组均未接触风险因素的 92 组数据也没有提供任何信息。优势比的计算是另外两个值的比值：病例暴露于风险因素但对照组未暴露于风险因素的配对除以对照组暴露于风险因素但病例未暴露于风险因素的配对。在本示例中，风险因素与疾病相关的优势比为 25/4 = 6.25。置信区间的公式比较复杂（见 S. Selvin《流行病学数据统计分析》第 2 版第 286 页）。优势比的 95% 置信区间为 2.158 至 24.710。

用 Prism 使用二项式检验计算 P 值

当您阅读 McNemar 检验时，大多数书籍都会解释如何进行卡方检验计算。Prism 不会这样做，但我们提供了一个 免费的网络计算器。 二项式检验问的是同样的问题，但更准确，尤其是对小型研究。请按照以下步骤使用 Prism：

1.创建整体部分数据表。

2.在 A 列的前两行中输入不一致配对的数量，本示例中输入 25 和 4。

3.单击分析并选择比较观察计数和预期计数的分析。

4.选择以百分比形式输入期望值，并输入 50 作为两个期望百分比。

5.选择二项式检验，而不是卡方检验。

6.对于样本数据，P 值小于 0.0001。P 值回答了这个问题：如果疾病与风险因素之间真的不存在关联，那么输入该分析的两个值相差如此之远，甚至更远的几率有多大？

使用 McNemar 检验用 QuickCalcs 计算 P 值

GraphPad 的免费网络 QuickCalc 使用卡方检验近似计算 McNemar 检验。将两个不一致的数字（25 和 4）分别称为 R 和 S。QuickCalc 使用此公式计算卡方检验：

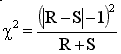
本示例中，卡方检验=13.79，有一个自由度。双尾 P 值为 0.0002。如果风险因素与疾病之间真的没有关联，那么观察到的优势比与 1.0（无关联）相差如此之远的概率为 0.02%。

上式使用了 Yates 修正（上式中的"-1"）。有时这一校正会显示为"- 0.5"。如果选择 Prism 的卡方检验法，则根本不会应用 Yates 修正。我们建议您选择二项式检验，这是一种精确检验，而不是选择卡方检验（这是一种近似方 法），并为是否应用 Yates 修正以及使用哪种修正而烦恼。