概览
用非线性回归拟合曲线时,最重要的一组结果是参数的 95% 置信区间。这些区间是根据标准误差计算出来的,而标准误差是基于一些数学简化计算出来的。它们被称为"渐近"或"近似"标准误差。计算时假定方程是线性的,但也适用于非线性方程。这种简化意味着置信区间可能过于乐观、过于狭窄,因此您的真实置信水平可能低于 95%。
如何知道置信区间是否真的有 95% 的置信度?这个问题没有通用的答案。但对于任何特定情况,您都可以通过模拟得到答案。本页将介绍如何使用 Prism 6 中新增的蒙特卡罗功能进行模拟。我们将模拟一条剂量反应曲线,并询问Hill斜率的95%置信区间有多精确。Christopolous 认为希尔斜率的分布可能不对称,并建议用Hill斜率的对数来拟合 (1)。
步骤 1.模拟第一次实验
在任意位置单击新建...分析,然后选择模拟 XY 数据。要完全按照本示例进行操作,请做出以下选择:
•X 值选项卡。从 X=-9 开始,每个 X 值递增 0.5,当 X 等于或超过 -3.0 时停止。
•方程选项卡。选择"剂量-反应-刺激"文件夹,并选择方程:log(激动剂) vs. 反应--变异性斜率。
•参数值选项卡。选择模拟一个数据集,有 3 个重复值。设置 Bottom=250, Top=5000, logEC50=-6 和 HillSlope=0.5。
•随机误差选项卡。随机误差为高斯(绝对值),SD=200。
第 2 步拟合第一个实验
1.在图表中单击"分析",选择"非线性回归"。或者点击工具栏分析部分的非线性回归快捷按钮。
2.在第一个(拟合)选项卡中,选择文件夹:剂量反应 - 刺激。然后选择方程:log(激动剂) vs. response --变异性斜率。您可以接受其他选项卡的所有默认值。
3.单击"确定",Prism 将根据数据拟合模型,并在图形上绘制曲线。
第 3 步再模拟几个数据集
注意Hill斜率,这是我们希望在本次模拟中研究的参数。要使用不同的随机数模拟新数据,请单击红色骰子图标,或下拉"更改"菜单并选择"再次模拟"。请注意,Hill 斜率发生了变化。
步骤 4.模拟多个数据集
从非线性回归结果开始,单击分析并选择蒙特卡罗模拟。
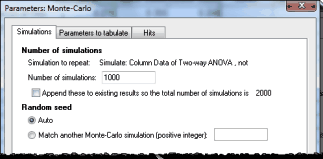
在第一个(模拟)选项卡上,选择希望 Prism 执行的模拟次数。本示例中输入 1000。
在第二个(要制表的参数)选项卡上,选择要制表的参数。选择的参数是 Prism 在分析数据时创建的分析常数列表。在本示例中,我们只想将 Hill 斜率的两个置信区间列表化。
在第三个("命中")选项卡上,定义一个标准,使给定的模拟结果成为"命中"。在本示例中,我们将"命中"定义为置信区间包含真实值 0.5(模拟中设置)。因此,当下限小于或等于 0.5,上限大于或等于 0.5 时,就定义为"命中"。
单击"确定",Prism 将运行模拟。依赖度取决于电脑速度,需要几秒或几十秒。
第 5 步蒙特卡洛结果
模拟结果只显示在一页上(因为我们在上面的"命中"选项卡中取消了报告单个模拟结果的所有选项)。
命中率为 0954。在本示例中,我们将"命中"定义为置信区间包含真实参数值。换句话说,在 1000 个模拟数据集中,HillSlope 的置信区间包含了 95.4% 的真实值(用于模拟)。(由于这些结果依赖于 Prism 生成的随机数,因此当您尝试按照本示例进行操作时,会得到一些不同的结果)。 这正是 95% 置信区间的预期结果,意味着可以相信这种设计的实验中的置信区间。对于这种实验设计,没有必要考虑用 Hill 斜率的对数来拟合。
步骤 6.尝试变化
如果这个结果的置信区间太宽(从 93.9% 到 96.6%),可以再迭代更多次(也许是 10,000 次)来运行蒙特卡罗模拟。
结论与您选择的实验设计和参数值有特异性。返回模拟,将 HillSlope 更改为 4.0。然后更改蒙特卡洛对话框,重新定义"命中",即置信区间括号内的真实值为 4.0。当下限小于或等于 4.0,上限大于或等于 4.0 时,就定义为"命中"。由于 HillSlope 如此陡峭,置信区间确实一点也不准确。95%"置信区间只包括 83.1% 模拟中的真实值(4.0)。将浓度数量增加一倍(在模拟 XY 数据对话框的 X 值选项卡中将 X 值的增量从 0.5 改为 0.25)可以解决这个问题。有了这么多数据点,95% 的模拟中 95% 的置信区间都包含了真实值。
通过改变模拟对话框中的选项,并通过蒙特卡罗模拟查看效果,可以设计出更好的实验。
另一个示例
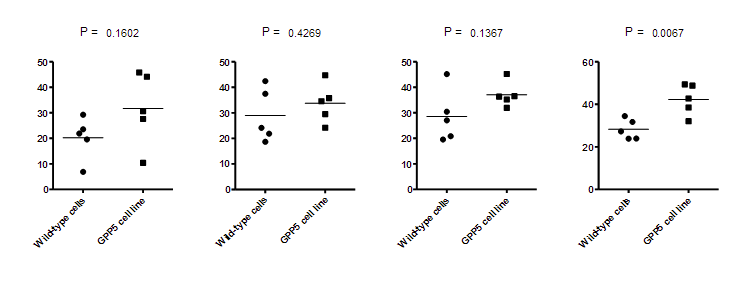
下面是另一个详细的示例,使用模拟来找出 t 检验的检验力。
参考资料
1.Arthur Christopoulos,Assessing the distribution of parameters in models of ligand-receptor interaction: to log or not to log,Trends in Pharmacological Sciences, Volume 19, Issue 9, 1 September 1998, Pages 351-357