概览
本示例将计算非配对 t 检验的检验力。不过,本示例的目标更为宽泛--展示使用 Prism 进行蒙特卡洛分析是多么容易,并向您展示蒙特卡洛分析是多么有用。
这里的问题是这样的:给定一定的实验设计和随机散点假设,非配对 t 检验得到小于 0.05 的 P 值从而被宣布为统计学显著的几率(检验力)是多少?
步骤 1.模拟第一次实验
在任意位置单击新建...分析,选择模拟列数据。选择模拟两组,每组 5 个值,分别从均值为 25 和 35、SD 为 10 的高斯分布群体中取样。
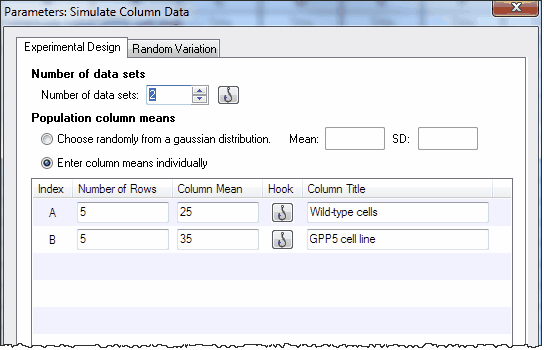
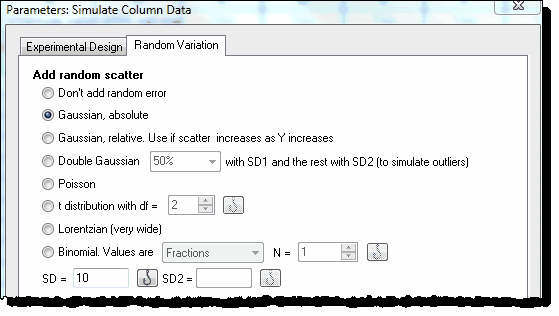
第 2 步用 t 检验分析数据
在模拟数据表中单击"分析",然后从列分析列表中选择 t 检验。接受所有默认选项,执行非配对 t 检验,报告双尾 P 值。
步骤 3.查看几个模拟结果
从结果中复制 P 值并粘贴到数据图表上。粘贴时会带有实时链接,因此如果数值发生变化,P 值也会随之变化。要使用不同的随机数模拟新数据,请单击红色骰子图标,或下拉"更改"菜单并选择"再次模拟"。
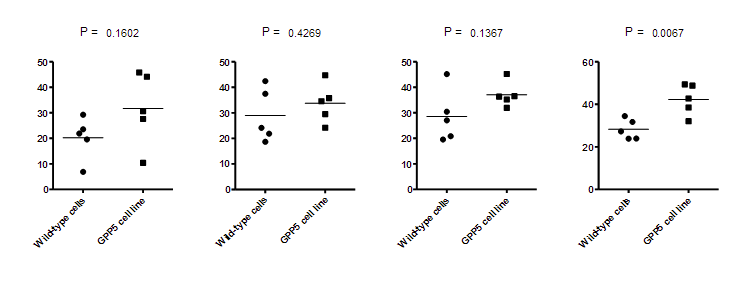
下面的布局显示了四个这样的图形,它们作为非链接图片放置在布局上,当图形发生变化时不会更新。尽管项目中只有一个图形,但这样就可以在布局中放置四个不同版本的图形(随机数据各不相同)。您可以看到,在数据随机变化的情况下,P 值变化很大。
步骤 4.蒙特卡罗模拟
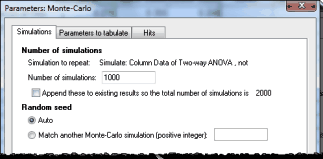
从 t 检验结果开始,点击分析并选择蒙特卡罗模拟。
在第一个(模拟)选项卡上,选择希望 Prism 执行多少次模拟。本示例使用了 1000 次模拟。
在第二个(要制表的参数)选项卡上,选择要制表的参数。选择的参数是 Prism 在分析数据时创建的分析常数列表。在本示例中,我们只想列出 P 值(来自比较均值的 t 检验;不要与来自比较方差的 F 检验的 P 值混淆)。
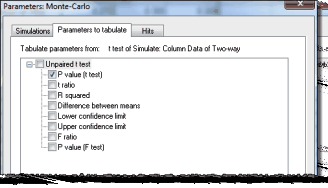
在第三个(命中)选项卡上,定义一个标准,使给定的模拟结果成为"命中"。在本示例中,我们将"命中"定义为 P<0.05 的统计学显著性。
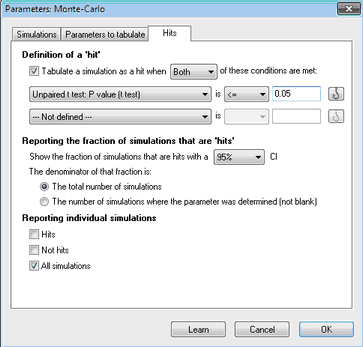
单击"确定",Prism 将运行模拟。依赖于电脑的运行速度,运行时间可能是几秒,也可能是几十秒。
第 5 步蒙特卡洛结果
P 值的分布
模拟结果显示在两页中。
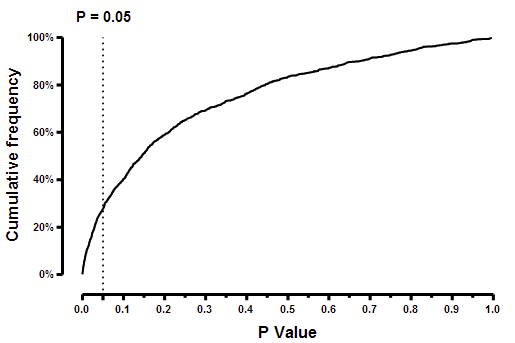
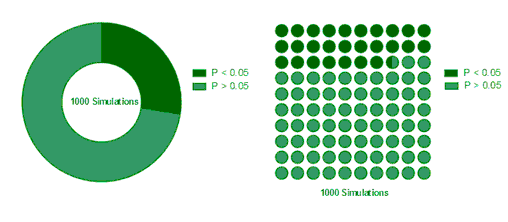
一页显示所有模拟的表列参数。在本示例中,我们只要求将 P 值列表,因此此表是 1000 个(要求的模拟次数)P 值的列表。要从该表中创建频率分布,请单击"分析",然后选择"频率分布"。选择累积频率分布。可以看到,大约四分之一的 P 值小于 0.05。
命中率
另一个结果表总结了命中率。在这组模拟中,27.5% 的模拟为命中(P 值小于 0.05),95% 的置信区间为 24.8% 至 30.4%。这些结果的另一种表述方式是,我们的实验设计的检验力为 27.5%。
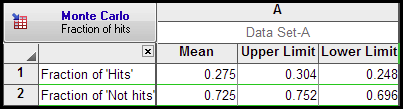
需要注意的是,模拟依赖于随机数的生成,而随机数是由你开始的时间初始化的。因此,如果你的结果可能与上表所示不完全相同。
如果我们进行了更多的模拟,置信区间当然会缩小。
从该表中,单击新建...现有数据表和图表,创建饼图或百分比图。
步骤 6.进一步探索
回到步骤 1,模拟一个更大的实验,比如每组 10 个值。或者 20 个或 100 个。这样检验力会提高多少?
尝试将"命中"的定义降低为 P 值小于 0.01,而不是 0.05。这对检验力有何影响?