双向方差分析确定一个反应如何受到两个因素的影响。本示例中,您可以测量男性和女性对三种不同药物的反应。
变异来源
双向方差分析将各值之间的总变异性分为四个部分。Prism 将行和列因素交互作用导致的变异性百分比、行因素导致的变异性百分比和列因素导致的变异性百分比制成表格。其余的变异是重复样本之间的变异(也称为残差变异)。
这些值(总变异的百分比)被 Sheskin 称为标准欧米茄平方 (公式 27.51 - 27.53),被 Maxwell 和 Delaney 称为R2(第 295 页)。还有人称这些值为 eta 平方或相关比。
方差分析表
方差分析表将测量值之间的总体变异性(以平方和表示)分解为四个部分:
•行与列之间的交互作用。这是行与行之间的差异,但每一列都不相同,相当于列与列之间的差异,但每一行都不相同。
•列之间的变异性。
•行间变异性。
•残差或误差。与行列间系统差异无关的重复样本间的差异。
方差分析表显示了平方和如何划分为四个部分。大多数科学家都会跳过这些结果,除非你对统计学有深入研究,否则这些结果并不能提供特别多的信息。对于每个分量,表中显示了平方和、自由度、均方差和 F 比。每个 F 比值都是该变异源的均方值与残差均方值之比(在重复测量方差分析中,一个 F 比值的分母是匹配的均方值,而不是残差均方值)。如果零假设成立,F 比值很可能接近 1.0。如果零假设不成立,F 比可能大于 1.0。F 比率本身并不能提供很多信息,但可用于确定 P 值。
P 值
双向方差分析将结果变量的总体变异性分成三个部分,外加一个残差(或误差)项。因此,它可以计算检验三个零假设的 P 值(重复测量双向方差分析又增加了一个 P 值)。
交互作用 P 值
零假设是:列(数据集)与行之间不存在交互作用。更准确地说,零假设是指列之间的任何系统差异对每一行都是相同的,行之间的任何系统差异对每一列都是相同的。通常,交互作用检验是三种检验中最重要的一种。 如果列代表药物,行代表性别,那么零假设是药物之间的差异对男性和女性是一致的。
P 值回答了这个问题:
如果零假设成立,那么随机抽样受试者,最后得到的交互作用与您观察到的一样多(或更多)的机会有多大?
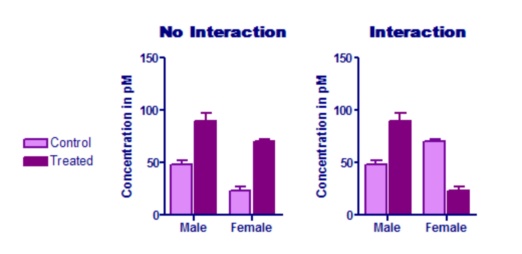
下图左侧显示没有交互作用。治疗对男性和女性的效果大致相同。右图则显示出巨大的交互作用。治疗效果在男性(治疗会增加浓度)和女性(治疗会降低浓度)中完全不同。在本示例中,男性和女性的治疗效果方向相反。但交互作用检验并不检验效果是否朝着不同的方向发展。它检验的是每一行(本示例中为每种性别)的平均治疗效果是否相同。
检验成对值需要输入重复值或平均值和 SD(或 SEM)以及 N。如果每行/列对只输入一个值,Prism 就会假定不存在交互作用,并继续进行其他计算。依赖度取决于您的实验设计,这一假设可能有意义,也可能没有意义。
列因子 P 值
零假设是,总体中每列(完全忽略行)的均值是相同的,我们看到的列均值之间的所有差异都是偶然造成的。在上面的示例图表中,对照组和治疗组的结果被输入不同的列(男性和女性被输入不同的行)。零假设是治疗无效,因此对照组和治疗组的数值差异只是偶然造成的。P 值回答了这个问题:如果零假设成立,那么随机获得的列均值与您观察到的列均值一样不同(或更大)的几率是多少?
在上图左侧示例图表中,列因子(处理)的 P 值为 0.0002。处理具有统计学显著影响。
在上图右侧示例图表中,列因子(治疗)的 P 值非常高(0.54)。平均而言,治疗效果与随机变异无异。但这个 P 值在本示例中意义不大。因为交互作用 P 值很低,所以可以知道治疗效果在每一行(本示例中为每个性别)都不一样。事实上,在本示例中,治疗对男性和女性的效果是相反的。因此,询问总体、平均治疗效果没有任何意义。
行因素 P 值
零假设是:在总体中,每一行(完全忽略列)的均值是相同的,我们看到的各行均值之间的所有差异都是由偶然因素造成的。在上面的本示例中,各行代表性别,因此零假设是男性和女性的平均回答相同。P 值回答了这个问题:如果零假设成立,那么随机得到的各行均值与您观察到的一样不同(或更大)的几率是多少?
在上述两个本示例中,行因素(性别)的 P 值都非常低。
数据汇总表
结果表中的这一小部分提供了以下内容的汇总:
•列数(列因子)
•行数(行因素)
•数值的数量
请注意,使用 "因子名称 "选项卡为列因子和行因子输入描述性名称,将在数据汇总表中显示输入的描述性名称。Prism 8.2 中为普通单向方差分析添加了这一功能。
多重比较检验
请注意,由双向方差分析产生的三个 P 值并没有进行三次比较校正。这样做似乎合乎逻辑,但在传统的方差分析中并没有这样做。
多重比较检验是统计检验中最容易混淆的课题之一。由于 Prism 为单向方差分析和双向方差分析提供了几乎相同的多重比较检验,因此我们合并了有关多重比较的信息。
参考文献
David J. Sheskin.参数和非参数统计程序手册》:第三版 IBSN:1584884401.