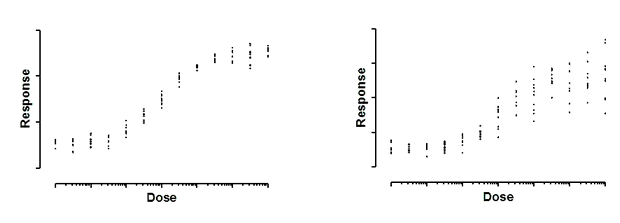
上面两幅图都显示了剂量反应曲线，每个反应点都有十个重复值进行测量。在左图中，这些重复值的标准偏差是一致的。沿曲线方向一直大致相同。在右图中，重复样本的标准偏差与 Y 值有关。随着曲线的上升，重复样本之间的差异也在增加。

这些数据都是模拟数据。在这两种情况下，重复样本间的差异都是从高斯分布中采样的。在左边的图表中，所有剂量的高斯分布的 SD 值相同。在右图中，SD 是平均 Y 值的一个恒定分数。当一个反应是另一个反应的两倍时，重复样本间的标准偏差也是两倍大。换句话说，变异系数 (CV) 是恒定的。

如果对右边的数据进行模型拟合，而不考虑散点随 Y 值增大而增大这一事实，会发生什么情况？ 考虑两个剂量，它们产生的不同反应相差 2 倍。对于较高的反应，重复样本与真实曲线的平均距离将是真实曲线的两倍。由于回归最小化的是这些距离的平方和，这些点对平方和的期望值将是平均 Y 值较小的点的四倍。换句话说，平均 Y 值是另一组两倍的一组重复样本的权重将是另一组的四倍。这基本上意味着，曲线拟合程序将更加努力地使曲线靠近这些点，而相对忽略 Y 值较低的点。您需要在较低的一组中添加四倍的重复数据，以平衡对平方和的贡献。

加权的目的是让曲线上任何位置的点对平方和的贡献相同。当然，随机因素会使某些点的散度大于其他点。但加权的目的是使这些差异完全随机，与 Y 值无关。"加权 "一词有点误导，因为其目的是去除 Y 值高的点的额外权重。真正的目的是取消权重。

Prism 在非线性回归的 "方法 "选项卡上提供了六种选择，并允许您测试适当的权重。