相对权重(按 1/Y2 加权)
在许多实验情况下,当 Y 值较高时,你期望点距曲线的平均距离(或者说距离的平均绝对值)较高。另一种说法是,当 Y 值越高时,您期望残差(各点与曲线的距离)的标准偏差越大--期望标准偏差与 Y 值成正比。
如果残差的标差与 Y 值有关,那么 Y 值越大的点往往离曲线越远(残差越大)。因此,这些点对平方和的贡献会更大,从而在计算中占主导地位。
解决方法不是最小化平方和,而是最小化加权平方和。换句话说,就是最小化数据 Y 值(Ydata)与曲线 Y 值(Ycurve)的相对距离。选择相对权重时,非线性回归会将这个量最小化:

左边最容易理解。计算每个点(在 Y 方向上)离曲线的距离,用该数值除以曲线的 Y 值,然后将该比值平方。将所有点的平方比相加。右边是等价的。它分别将分子和分母平方,然后计算这两个平方值的比值。这是大多数数学统计学家对加权的思考方式,所以相对权重也叫Y2 加权。
泊松加权
按 1/Y 加权是最小化实际距离平方和最小化相对距离平方之间的折中。当 Y 值呈泊松分布时,适合采用 1/Y 加权。当 Y 值为放射性计数,且大部分散点是由计数误差造成时,就会出现这种情况。在泊松分布中,数值的标准误差等于该数值的平方根。因此,需要用数据与曲线之间的距离除以数值的平方根,然后将结果平方。下式显示了 Prism 最小化的量,并说明了为什么称为按 1/Y 加权(但 Prism 实际是按 Y 的绝对值加权)。
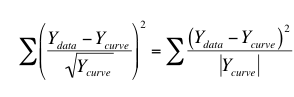
一般加权
下面的前三个等式显示了绝对权重、泊松权重和相对权重之间的关系。请注意,将任何值检验力为零的结果都是 1.0,因此左边等式的分母总是等于 1.0。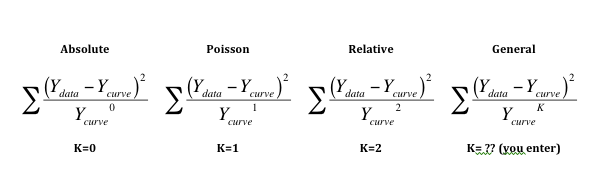
右边的等式显示的是一般加权。输入 K 可以自定义加权方案,以适应您的数据。一般情况下,K 值在 1.0 和 2.0 之间时采用这种方法。 下面的参考文献 1 就采用了这种方法。
如果您想通过实验确定 K 的最佳值,也可以这样做:
1.在沿曲线的许多点上收集大量(十几个,甚至几十个)重复数据。
2.用常规方法绘制数据图,确保数据看起来正确无误。
3.绘制第二张图表,忽略 X 值(时间或浓度......)。相反,在这个新图表中,X 是第一个图表中每个点的重复 Y 值的均方值的对数,而这个新图表中的 Y 是重复值的方差(标准偏差的平方)的对数。您可以使用自然对数或以 10 为底的对数。只要两个对数的基数相同,就没有关系。
4.使用线性回归法在此图上拟合一条直线。由于这条直线周围的高斯变化假设是可疑的,因此应使用非线性回归并选择稳健的拟合。
5.这条回归线的斜率为 K。如果 K 接近 0.0,则 SD 不随 Y 变化,因此无需加权。如果 K 接近 2.0,则标准偏差与 Y 成正比,适合进行相对权重。如果 K 接近 1.0,则选择泊松加权。如果 K 有其他值,则使用一般加权法,并将该 K 值作为常数输入。
请注意,如果 Ycurve 为负值,Prism 实际取 Ycurve 的绝对值到 K 的检验力。
Prism 中罕见的权重选择
按 1/X 或1/X2加权的选择会使图形左侧的点比右侧的点权重更大。这在某些领域的生物分析数据拟合直线时很常见。
Prism 还提供了按标准偏差平方的倒数加权的选项。该选项可将以下情况降至最低:
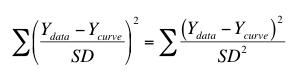
当您设置了输入 SD 值的数据表格式,但又输入了您根据对实验系统中散差(或误差)产生方式 的理解而在其他地方计算出来的值时,这种方法最为有用。 您输入的 "标差 "值应该是计算得出的加权因子,而不是数据的实际标差。
如果您在 "SD "子列中输入实际 SD 值,或输入重复值以便 Prism 计算 SD,那么 Prism 将使用这些实际 SD 值作为加权因子。这一点比听起来要有用得多。对于中小规模的样本量,随机抽样的 SD 值会跳动很大,因此使用这些随机 SD 值来加权是不合适的。加权应该按照预测标差而不是实际标差(实际标差受随机因素影响)。
当然,如果输入的 SD 值为零,则不可能使用 SD 加权。如果 Prism 是通过重复样本计算自标度,而只有一个重复样本,或者所有重复样本完全相同(因此它们的自标度等于零),也无法进行加权。
Prism 在第一次迭代时不使用加权
在一种情况下,根据曲线的预测 Y 值加权会导致问题--当初始值非常糟糕时。初始曲线可能与点相差很远,在某些情况下,某些 X 值的 Y 值可能为 0,这样就不可能按 1/Y 或 1/Y2 加权。 为了提高拟合值,即使初始值生成的曲线与数据相差甚远,Prism 也会在第一次迭代时不使用权重。第一次迭代会使曲线更接近点。此后,Prism 将使用您指定的权重函数。从本质上讲,Prism 会将一次迭代的非加权拟合结果作为加权拟合的初始值。
参考
1.LM Lavasseur, H Faessel, HK SLocum, and WR Greco, Implications for Clinical Pharmacodynamic Studies of the Statistical Characterization, of an In Vitro Antiproliferation Assay, J. Pharmacokinetics and pharmacodynamics, 26: 717-733, 1998.