为了让您了解数学模型的工作原理，下面简要介绍三种常用模型。

光密度与浓度的函数关系

背景

比色化学分析基于一个简单的原理。在样品中加入适当的反应物，启动化学反应，反应产物就会着色。当反应终止时，有色产物的浓度与要检测的物质的初始浓度成正比。

模型

由于光密度与有色物质的浓度成正比，因此光密度也将与您要检测的物质的浓度成正比。

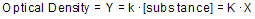
现实检验

从数学上讲，该方程式适用于任何 X 值。

•负 X 值毫无意义，因为浓度不可能为负。

•在物质浓度较高时，反应不再受物质浓度的限制，模型可能会失效。

•如果溶液变得很暗（光密度很高），几乎没有光到达检测器，模型也可能在高浓度下失效。此时，仪器的噪声可能会超过信号。

一个模型只在一定的数值范围内工作是很正常的。您只需了解其局限性，不要试图在其有用范围之外使用模型。

指数衰减

指数方程是指某事物发生的速度与剩余量成正比。本示例包括配体与受体的解离、放射性同位素的衰变以及药物的新陈代谢。用微分方程表示：

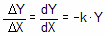
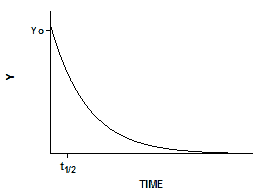
将微分方程转换成定义不同时间 Y 的模型需要一些微积分。只有一个函数的导数与 Y 成正比，即指数函数。对方程两边进行积分，得到一个新的指数方程，该方程将 Y 定义为 X（时间）、速率常数 k 和 Y 在零时的值Y0 的函数。

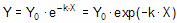
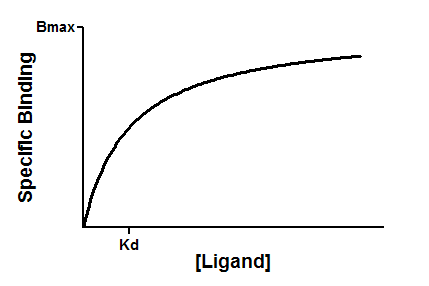
平衡结合

当配体与受体交互作用时，或者当底物与酶交互作用时，结合遵循质量作用定律。

测量结合量即 RL 复合物的浓度，将其绘制在 Y 轴上。我们可以假设加入的配体量与游离配体的浓度 L 相同，因此这构成了 X 轴。通过一些简单（但繁琐）的代数运算，可以得出以下等式：