Prism 如何报告斜率和截距

Prism 首先报告斜率和截距的拟合优度值及其标准误差。它还会报告 X 截距和斜率的倒数。在这些值下方，它会报告斜率和截距的 95% 置信区间。

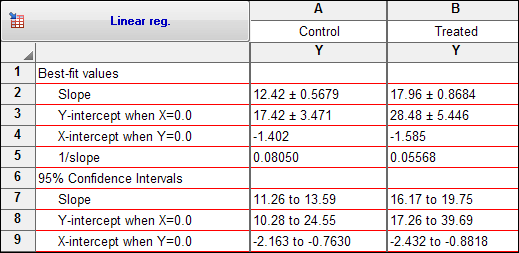
在结果页面的底部，斜率和截距会以定义拟合优度线的方程形式再次报告。您可以复制该等式并粘贴到图表上或手稿中。

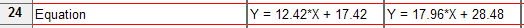
解读斜率和截距

斜率表示直线的陡度。它等于 X 轴每变化一个单位时 Y 轴的变化量，用 Y 轴的单位除以 X 轴的单位来表示。如果斜率为正，则 Y 随 X 的增加而增加。如果斜率为负，则随着 X 的增大，Y 会减小。

Y 截距是 X 等于零时直线的 Y 值。它定义了直线的高程。

解读标准误差和置信区间

斜率和截距的标准误差值可能很难解读，但其主要目的是计算 95% 置信区间。

如果接受线性回归的假设，则斜率的 95% 置信区间包含斜率真值的概率为 95%，截距的 95% 置信区间包含截距真值的概率为 95%。置信区间的宽度由数据点的数量、它们与直线的距离以及 X 值的间距决定。

Prism 也可以绘制置信带或预测带。

X 截距及其置信区间

如果选中线性回归参数对话框中的选项，GraphPad Prism 会报告 X 截距的 95% 置信区间。

X 截距的 95% 置信区间不是围绕 X 截距对称的。如下图所示，它在一个方向上比另一个方向更远。

 

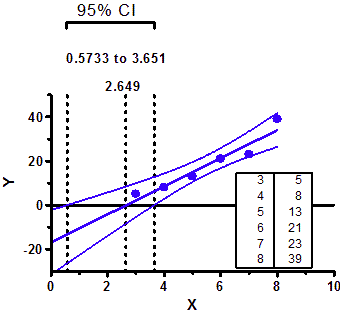
沿着 Y=0 的基线从左向右看。最佳拟合优度线（蓝色曲线）的 95% 置信带之间的区域就是 X 截距的 95% CI。可以看到，这个置信区间（最外侧的两条虚线之间）并不是围绕 X 截距（中间的虚线）对称的。

如果只有少数几个点有大量散点，这种不对称就会非常明显，而如果有大量点有少量散点，这种不对称就会几乎不明显。

由于不确定性不对称，报告 X 截距的标准误差很少有意义。报告 95% 置信区间的两端要好得多，Prism 也会报告。如果真的想计算 X 截距的单一标准误差，可以选择非线性回归，并将此用户定义方程拟合到数据中：

Y = 斜率*（X-X 截距）

Prism 将报告 X 截距的拟合优度值以及 SE 和 95% 置信区间。由于置信区间是根据 SE 值计算得出的，它将围绕 X 截距对称，因此不如线性回归报告的不对称区间准确。