引言

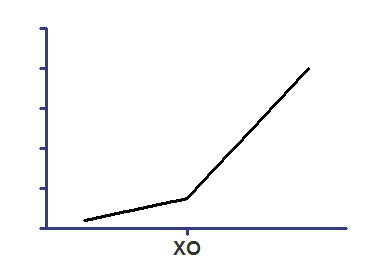
分段回归通常也称为 "分片"回归或分段回归。使用这种方法，一条直线拟合 X 值小于某个指定值 X0 的所有数据点，另一条直线拟合 X 值大于 X0 的所有数据点，同时确保两条直线在 X0 处相交。

分段线性回归有用的一个常见本示例是，当 X 为时间时，您在 time=X0 时做了一些事情来改变直线的斜率。也许你注射了药物，或者快速改变了温度。在这种情况下，你的模型确实有两个斜率，并有一个尖锐的过渡点。

在其他情况下，真实模型的斜率是逐渐变化的。数据拟合的是一条曲线，而不是两条直线。在这种情况下，用分段线性回归拟合数据是没有帮助的。

注意事项

不要使用分段线性回归分析双相 Scatchard 或 Lineweaver-Burk 图。双相斯卡查德图是一条曲线，而不是两条相交的直线。没有突然的断点。您应该将原始数据拟合为双位点结合曲线。

步骤

创建 XY 数据表。将时间输入 X 列，将测量结果输入 Y 列。如果有多个实验条件，则将第一个条件放入 A 列，第二个条件放入 B 列，等等。

输入数据后，点击分析，选择非线性回归，选择线性的面板方程，然后选择分段线性回归。

模型

Y1 = 截距1 + 斜率1*X 

YatX0 = 斜坡 1*X0 + 截距 1

Y2 = YatX0 + slope2*(X - X0) 

y = if(x<x0, y1, y2)

 

方程的第一行根据截距和斜率定义了第一条线段。

方程的第二行计算该线段右端第一次回归的 Y 值，此时 X=X0。

等式的第三行计算第二个回归分段。由于我们需要的是一条连续的直线，所以第二段左端的 Y 值必须等于第一段右端的 Y 值（YatX0）。第二段回归线上任何其他位置的 Y 值都等于 YatX0 加上第二段回归线带来的增加值。该增加值等于第二段的斜率（sope2）乘以从 X0 到 X 的距离。

如果 X 小于 X0，则 Y 等于 Y1。否则 Y 设置为 Y2。

解读参数

Intercept1是第一条线段与 Y 轴段相交的 Y 值。

Slope1是第一条线段的斜率，用 Y 单位除以 X 单位表示。

Slope2是第二条线段的斜率，用 Y 单位除以 X 单位表示。

X0是两条线段相交处的 X 值。通常情况下，您会希望将其限制为一个恒定值，该值等于您应用实验干预的时间。

 

扩展到三个线段

Prism 不包含三段分段回归方程，但您可以将此方程作为用户自定义方程输入：

Y1 = 截距 1 + 斜率 1*X

YatX0 = 截距1 + 斜率1*X0 

Y2 = YatX0 + slope2*（X - X0）

YatX1 = YatX0 + slope2*（X1-X0）

Y3 = YatX1 + slope3*（X - X1）

y = if(x<x0, y1, if(x<x1, y2, y3))

.