在有非线性坐标轴的图形上拟合直线

非线性回归分析拟合的是数据，而不是图形。如果选择概率 Y 轴，则数据点构成直线的图形会遵循非线性关系。Prism 的 "线性"方程集包含一些方程，可以让您将非线性模型拟合到 Y 轴为概率轴时显示为线性的图形中。在这种情况下，线性回归会根据数据拟合出一条直线，但由于一个轴（或两个轴）不是线性的，所以图形看起来会是弯曲的。相反，根据适当的非线性模型进行非线性回归，则会在这些坐标轴上绘制出一条看似直线的曲线。

输入和拟合数据

1.创建 XY 表格，输入 X 和 Y 值。

2.转到图表，双击坐标轴，弹出设置图表格式对话框。将 Y 轴改为概率刻度。

3.单击分析，选择非线性回归（而非线性回归），然后从方程的 "线性"部分选择累积高斯分布方程之一。

方程

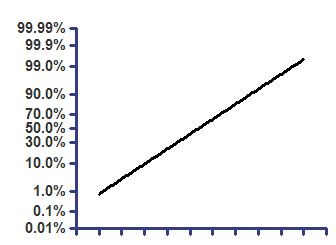
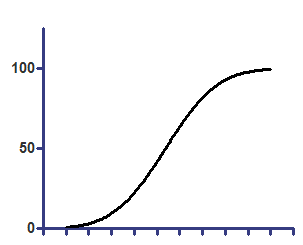
累积高斯分布 - Y 值为百分比

顶部=100

z=(X-Mean)/SD

Y=Top * zdist(z)

 

 

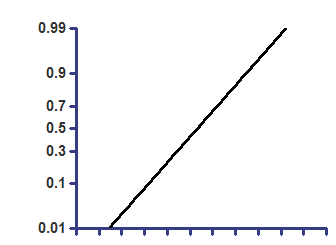
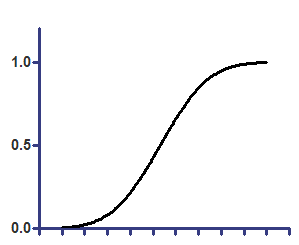
累积高斯 - Y 值为分数

顶部=1

z=(X-Mean)/SD

Y=Top * zdist(z)

 

参数

平均值是原始分布的平均值，频率分布就是根据原始分布创建的。

标准偏差是原始分布的标准偏差。

这两个参数的单位都与图表中绘制的 X 值相同，即与频率分布的原始分布中的 Y 值相同。