关于R2的问答
R2表示什么
•R2值用于量化拟合优度。它将您的模型拟合度与通过所有 Y 值均值的水平线的拟合度进行比较。
•您可以将R2视为模型(方程)所能解释的 Y 总方差的一部分。有了实验数据(和合理的模型),您总会得到介于 0.0 和 1.0 之间的结果。
•另一种思考R2的方法是实际值和预测 Y 值之间相关系数的平方。
R2的取值范围有多大?
答案很简单,R2通常是介于 0.0 和 1.0 之间的分数,没有单位。但也有特殊情况:
•当曲线经过每个点时,R2等于 1.00。但如果在相同的 X 值上有重复的 Y 值,曲线就不可能经过每一点,因此R2必须小于 1.00。
•当R2等于 0.0 时,拟合优度曲线对数据的控制并不比通过所有 Y 值平均值的水平线更好。在这种情况下,了解 X 并不能帮助预测 Y。
•当你选择了一个非常不合适的模型或施加了愚蠢的约束条件时(通常是错误的),拟合优度曲线会比水平线拟合得更差。在这种情况下,R2将为负值。是的,这看起来很奇怪,但R2并不是任何东西的平方,而且这也是可能的。详情请见本页底部。
•您可能会看到R2的值可能大于 1.0。只有在使用无效方程时才会出现这种情况,因此结果是错误的。
r2还是R2?
按照传统,统计学家用大写字母 (R2) 表示非线性和多元线性回归的结果,用小写字母 (r2) 表示线性回归的结果,但这只是一种没有区别的区分。
为什么有人建议不报告非线性回归的R2?
Minitab 不报告非线性回归的R2,因为他们认为这太容易引起误解。Kvalseth(1) 也对其使用提出了警告。问题包括
•在线性回归中,R2比较的是最佳拟合回归线与水平线(强制斜率为 0.0)的拟合优度。水平线是回归线最简单的情况,所以这是有道理的。对于非线性回归中使用的许多模型,水平线根本无法从模型中生成。因此,将所选模型的拟合结果与水平线的拟合结果进行比较在数学上并不合理。因此,SAS 将该值称为 "伪R2"。
•使用R2比较其他模型的拟合效果很有诱惑力。您不应该这样做。调整后的 R2 更适合这种用途,但并不理想。Prism 提供了两种比较替代模型拟合度的更好方法。 模型选择必须评估权衡--更复杂的模型通常拟合得更好,但它们有更多的参数。Prism 提供的两种方法都能评估这种权衡。R2则不然。R2几乎总是随着复杂模型的增加而增加,即使模型正确的可能性较低。不要根据R2 来选择模型。
•参数数相同的两个模型对数据的拟合程度可能完全不同,AICc 方法会告诉您其中一个模型更有可能是正确的。但是,R2值可能只在小数点后的第三或第四位有变化。
•高R2说明曲线非常接近点。但这并不意味着拟合在其他方面 "很好"。参数的拟合优度值可能毫无意义(例如,负速率常数),或者置信区间可能非常宽。拟合可能模糊不清。您需要查看所有结果来评估拟合结果,而不仅仅是R2。
为什么 Prism 会报告非线性回归的R2?
Prism 默认计算并报告R2。您可以在非线性回归对话框的 "诊断 "选项卡中关闭报告R2,并将该偏好设置为未来拟合的默认值。
很多人发现R2在这种情况下非常有用:当您运行一系列实验时,您希望确保今天的实验与其他实验一致。本示例中,如果你总是得到 0.90 到 0.95 之间的R2,但今天却得到了 R2=0.75,那么你就应该起疑心,仔细观察该实验所使用的方法或试剂是否出了问题。如果新员工带来的结果显示,使用同一系统的R2为 0.99,那么你就应该仔细看看有多少 "异常值 "被剔除了,是否有些数据是编造的。
我认为这是R2真正有用的唯一方法,但它对这一目的非常有用。
如何计算R2-- 非加权拟合
R2是根据非线性回归确定的拟合优度曲线上各点距离的平方和计算得出的。这个平方和值称为 SSreg,单位是 Y 轴的平方。为了将R2转化为分数,需要将结果归一化为各点距离通过所有 Y 值均值的水平线的平方和。该值称为 SStot。如果曲线与数据拟合得很好,SSres 就会比 SStot 小很多。
下图说明了R2 的计算。两个面板显示的是相同的数据和拟合优度曲线。左侧面板还显示了所有 Y 值平均值的水平线,以及显示每个点离所有 Y 值平均值距离的垂直线。这些距离的平方和(SStot)等于 62735。右侧面板显示了每个点与拟合优度曲线的垂直距离。这些距离的平方和(SSres)等于 4165。
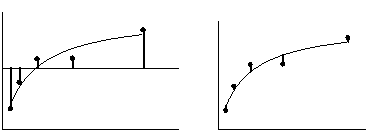
R2用以下公式计算
R2= 1.0 - (SSresiduals/SStotal) =1.0-4165/62735= 0.9336
这是 Kvalseth(1)的方法 1。
如果共享参数(执行全局非线性回归),上式中的 SSResiduals 是 Prism 在全局结果列中报告的共享参数拟合模型的平方和,SSTotal 是(每个数据集的)每个 Y 值围绕(所有数据集的)所有 Y 值均值的平方和。
如何计算R2-- 加权拟合
计算加权非线性拟合的R2似乎没有既定的方法。Prism(自 6.00 版起)的计算方法如下。但请注意,Prism 早期版本计算加权拟合R2的方法有所不同。
1.使用相对 (1/Y2) 或泊松 (1/Y) 或一般 (1/XK) 加权拟合模型,计算加权平方和 (wSSmodel)。这是模型残差的加权平方和。
2.请记住每个点的权重。
3.将数据拟合为水平线模型(Y= 平均值 + 0*X),每个点的权重与步骤 1 中使用的相同。 这就是水平线的加权残差平方和(wSShorizontal)。
加权R2为
1.0 - (wSSmodel/wSShorizontal)
请注意,权重仅在拟合模型时计算。Prism 不会计算拟合水平线时的权重,而是使用与拟合模型时完全相同的权重。这样可以确保两次拟合的权重总和相同。
更多详情,Prism 使用 Willett 和 Singer (2) 中的公式 4。
R2怎么会是负数?
平方怎么会是负值?其实,R2并不是任何东西的平方。它是通过减去两个值计算出来的。如果 SSres 大于 SStot,R2将为负值(见上式)。
怎么会这样呢?SSres 是各点与拟合优度曲线(或直线)垂直距离的平方和。SStot 是各点距 Y 均方值水平线的垂直距离平方和。当拟合优度线或曲线比水平线更不拟合数据时,SSres 将超过 SStot。
当最佳拟合直线或曲线与数据的拟合优度很差时,R2将为负值。只有当您拟合的模型选择不当(可能是错误的),或者您对模型应用了不合理的约束条件(可能您输入的是正数,而您本意输入的是负数)时,才会出现这种情况。 例如,如果您将剂量反应曲线的 Hill 斜率限制为大于 1.0,但实际上曲线是在走下坡路(因此 Hill 斜率是负的),那么最终您可能会得到一个负的R2值和无意义的参数值。
下面是一个简单的本示例。蓝线是一条直线的拟合,当 X=0 时,该直线被约束在 Y=150 处截距 Y 轴。SSres 是红点到这条蓝线的距离平方和。SStot 是红色点距绿色水平线距离的平方和。由于 Sres 远远大于 SStot,因此R2(对蓝线的拟合)为负值。
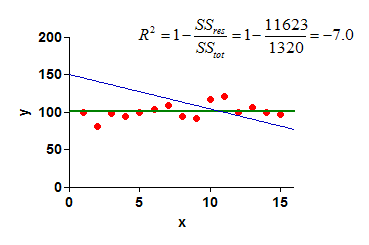
如果R2为负值,请检查您是否选择了合适的模型,并正确设置了任何约束条件。
1.Kvalseth, T.O. (1985)关于R2 的注意事项。美国统计学家》,39,279-285。
2.Willett, J.B. and Singer, J.D. (1988).Another Cautionary Note aboutR2: Its Use in Weighted Least-Squares Regression Analysis.The American Statistician 42: 236.