R2可以量化模型与数据的拟合程度。在比较模型时，参数越多的模型越能弯曲和扭曲，从而更接近点，因此 R2 几乎总是越高。这有点误导。

调整后的R2考虑了回归拟合的参数数，因此可以在不同参数数的模型之间进行比较。这里比较了普通R2和调整后 R2 的等式（SSresiduals 是曲线 Y 值与数据之间差异的平方和；SStotal 是整体 Y 均值与每个 Y 值之间差异的平方和；n 是数据点的数量，K 是拟合参数的数量）：

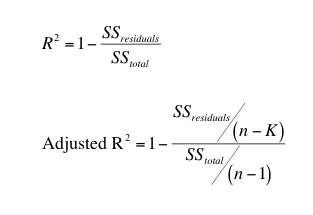
只要参数数（K）大于 1，调整后的R2就小于普通R2。

使用调整后的 R2 比较其他模型的拟合优度优于使用 R2（绝对不能使用 R2），但不如使用额外的平方和 F 检验或 Prism 内置的 AICc 方法。