额外的平方和 F 检验比较了用最小二乘回归拟合的两个嵌套模型的拟合情况。嵌套是指一个模型（较简单的模型，即下面的模型 1）是另一个模型（较复杂的模型，即下面的模型 2）的特例。

如果较简单的模型是正确的，那么平方和的相对增加（从较复杂的模型到较简单的模型）预计等于自由度的相对增加。换句话说，如果较简单的模型是正确的，则您预期

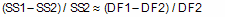
SS1 是较简单模型的平方和（会较高），SS2 是较复杂模型的平方和。回想一下，自由度等于数据点数减去参数数。更复杂的模型有更多的参数，因此自由度更小。

如果更复杂的模型是正确的，那么您期望平方和的相对增加（从复杂模型到简单模型）大于自由度的相对增加：

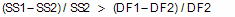
F 比量化了平方和的相对增加与自由度的相对增加之间的关系。

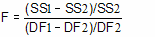
该等式通常以等价形式表示：

F 比率总是与分子的一定自由度数和分母的一定自由度数相关联。这个 F 比的分子有 DF1-DF2 个自由度，分母有 DF2 个自由度。

如果简单模型是正确的，您就会得到一个接近 1.0 的 F 比值。如果比值远大于 1.0，则有两种可能：

•更复杂的模型是正确的。

•更简单的模型是正确的，但随机散点导致更复杂的模型拟合得更好。P 值告诉您这种巧合的罕见程度。

P 值回答了这个问题：

如果模型 1 确实是正确的，那么随机获得的数据比模型 2 更符合的概率有多大？

如果 P 值较低，则得出结论：模型 2 在统计学上显著优于模型 1。否则，得出结论：没有令人信服的证据支持模型 2，因此接受更简单的模型（模型 1）。