当 X 值是剂量或浓度的对数时，使用该方程。当 X 值为浓度或剂量时，使用相关方程。

引言

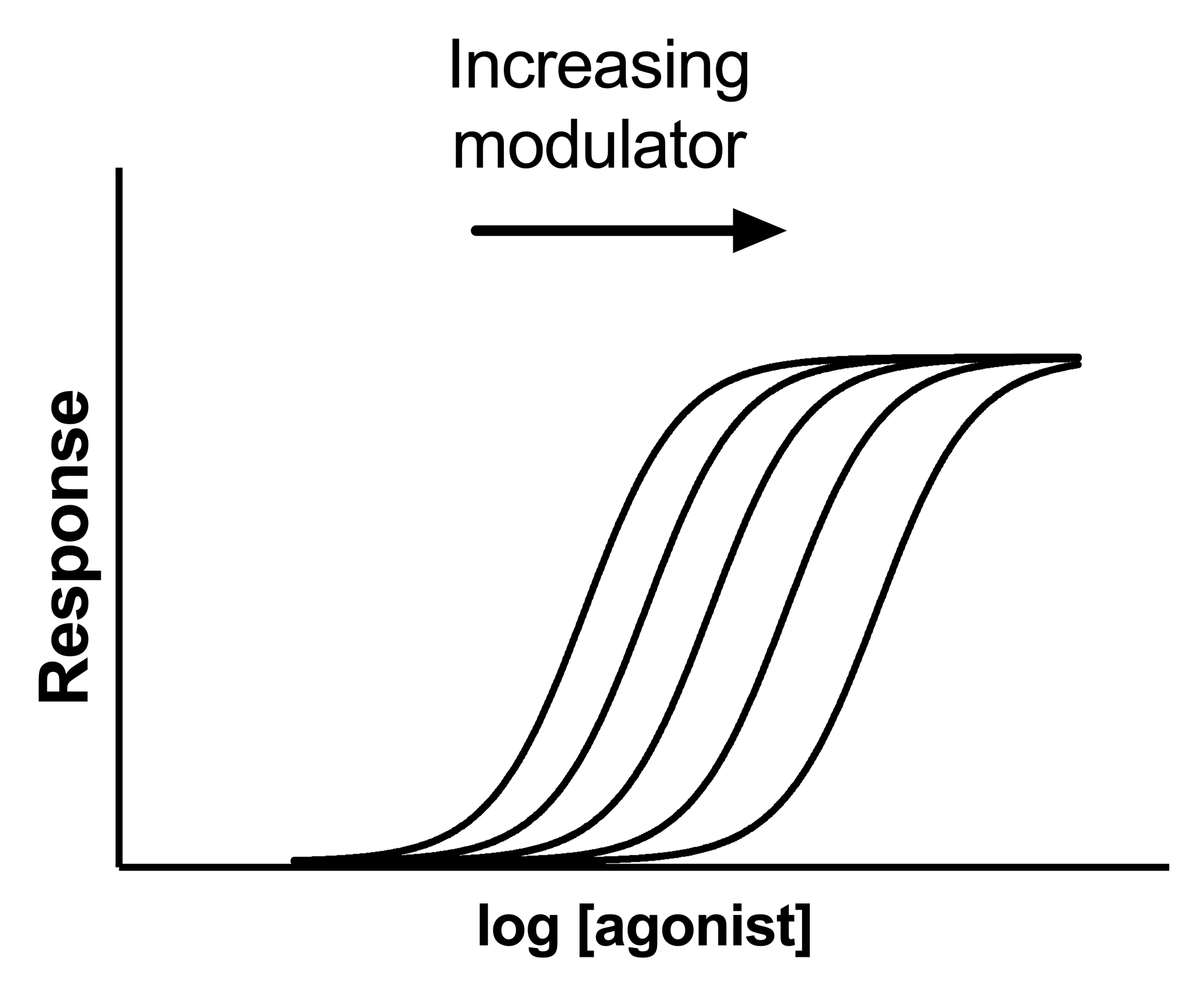
当结合实验中存在竞争性抑制剂时，它会与激动剂竞争结合到受体上，并使剂量反应曲线向右移动而不改变最大反应（在激动剂浓度足够高的情况下，竞争性抑制剂的影响可以被克服，最大反应仍然可以得到）。这种分析方法通过全局拟合多条曲线来实现，其中一条曲线拟合无抑制剂的值，其他曲线拟合不同浓度的竞争性抑制剂的值。通过全局拟合这些曲线，可以确定竞争性抑制剂的亲和力。

具体步骤

1.创建一个 XY 数据表，其中包含与您的实验设计相匹配的子列。

2.在 X 中输入激动剂配体浓度的对数。本示例中，如果浓度为 1nM，则输入 -9，不要输入 1e-9。

3.以任何方便的单位在 Y 中输入反应。在 A 栏输入不含抑制剂的数据，在 B 栏输入恒定抑制剂浓度下收集的数据。如果有数据，重复 C、D、E...列，每列使用不同浓度的抑制剂。

4.以摩尔为单位输入抑制剂浓度，作为数据表的列标题。如果浓度为 1nM，则在列标题中输入 "1e-9 "或 "0.00000001"。不要输入"-9"。不要忘记在数据集 A 的列标题中输入 "0"，因为这些是不含抑制剂的控制数据。在列标题中输入的这些值将在分析中使用；它们不仅仅是标签，因此需要以正确的格式输入。

5.在数据表中点击分析，选择非线性回归，然后选择方程面板： 剂量-反应-特殊，X 为对数（浓度）。然后选择Gaddum/Schild EC50 shift，X 为对数（浓度）。

6.考虑将参数 HillSlope 和 SchildSlope 限制为 1.0 的标准值。如果您没有很多数据点，因此无法拟合这些参数，这一点尤其有用。

单位说明

•在书写此方程时，X 值以激动剂浓度的对数输入，而列标题则以拮抗剂浓度输入。这只是方程的书写方式。如果您想克隆这个方程并采用不同的写法，也是很容易的。Prism 还提供了 一个相关方程 ，其中 X 值作为激动剂浓度输入。

•EC50 将以您输入 X 值时所用单位的反比来报告。如果您输入的 X 值为 log(摩尔)，那么 EC50 将以摩尔为单位。如果您输入的 X 值为 log（剂量，单位为毫克），那么 EC50 将以毫克为单位。

•pA2 是将曲线移动 2 倍所需的拮抗剂浓度的负对数。该浓度的单位与您在列标题中输入拮抗剂浓度时使用的单位相同。如果您在列标题中输入的浓度单位是 nM，那么 pA2 就是 nM 的负对数。如果以 mg/kg 为剂量输入浓度，则 pA2 为 mg/kg 的负对数。

•如果要将 pA2 转换为浓度，首先要翻转符号（乘以-1），然后取反对数（十的检验力）。如果您也想将置信区间转换为浓度，请注意符号的翻转也会改变置信区间的顺序，因此 "下"置信区间实际上是上限，而 "上"置信区间实际上是下限。Prism 将此值报告为 A2。

模型

EC50=10^LogEC50

Antag=1+(B/(10^(-1*pA2)))^SchildSlope

LogEC=Log(EC50*Antag)

Y=Bottom + (Top-Bottom)/(1+10^((LogEC-X)*HillSlope))

 

解读参数

EC50 和LogEC50：EC50 是指在没有抑制剂的情况下，能产生半数最大反应的激动剂浓度。对数 EC50 的单位与输入 X 值时使用的单位相同。EC50 是这些单位的反对数。

pA2是将剂量反应曲线移动 2 倍所需的拮抗剂浓度的负对数。 如果 SchildSlope 固定为 1.0，它就是 pKb，即抑制剂与受体结合的平衡解离常数（摩尔）的负对数。当 SchildSlope 限制为 1.0 时，Prism 会同时报告pA2和logKb。这些单位与您在数据表中作为列标题输入浓度时所使用的单位成对数关系。

A2是将剂量反应曲线移动 2 倍所需的拮抗剂浓度。 如果 SchildSlope 固定为 1.0，它就是 Kb 或抑制剂与受体结合的平衡解离常数（摩尔）。当 SchildSlope 限制为 1.0 时，Prism 将报告Kb，否则 Prism 将报告A2。单位与您在数据表中作为列标题输入浓度时使用的单位相同。

HillSlope描述曲线族的陡度。HillSlope 为 1.0 是标准值，您应考虑将 Hill 斜率限制为 1.0 的恒定值。

SchildSlope 量化了偏移与竞争交互作用预测的对应程度。如果竞争者具有竞争性，SchildSlope 将等于 1.0。您应考虑将 SchildSlope 限制为 1.0 的恒定值。如果不对 SchildSlope 进行约束，那么拮抗剂项就会包含一个以 S 为检验力的表达式，其中 S 表示 Schild 斜率因子。如果右移幅度大于竞争交互作用的预测值，则 S 将大于 1；如果右移幅度小于竞争交互作用的预测值，则 S 将小于 1。

顶部 和 底部 是以 Y 轴为单位的高原。

注

•所有六个数据集都是共享的，因此您只会看到每个参数的一个拟合优度值，而不是每个数据集的一个。

•Prism 不会报告每条曲线的 EC50，只会报告第一条曲线（没有任何拮抗剂的曲线）的 EC50。

•模型中的变异性 B 被定义为数据集常数，其值来自列标题。结果页面将显示这些 B 值。请确保它们是每个数据集中使用的拮抗剂浓度（而不是浓度的对数）。

 

Schild 模型何时有效？

Colquhoun (1) 指出，只要能做出以下假设，Schild 模型就是有效的：

•拮抗剂 B 是真正的拮抗剂，单独使用不会改变受体的构象。

•激动剂 A 和拮抗剂 B 在每个结合位点的结合是相互排斥的。

•B 与每个结合位点的亲和力相同。

•如果 A 对每个结合位点的占有率相同，则无论 B 占有多少结合位点，观察到的反应都是相同的。

•在平衡状态下进行测量。

 

1.Colquhoun, D..为什么 Schild 方法比 Schild 实现的方法更好？Trends Pharmacol Sci (2007) vol. 28 (12) pp.