当 X 值为浓度时，使用该方程。当 X 值是浓度或剂量的对数时，使用相关方程。

引言

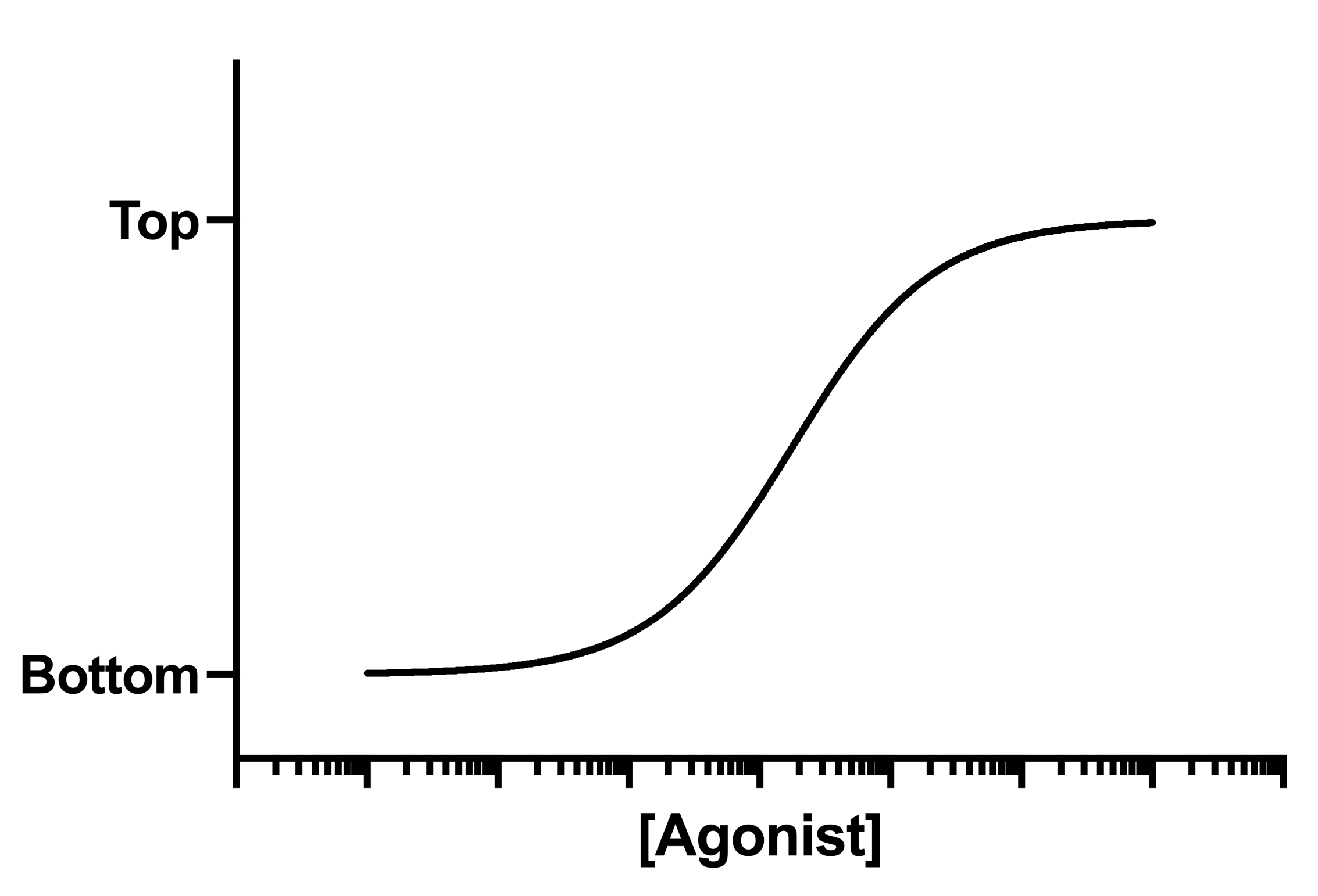
许多对数（剂量）反应曲线都遵循我们熟悉的对称西格玛形状。我们的目标是确定激动剂的 EC50 值，即在基础反应（底部）和最大反应（顶部）之间的中点引起反应的浓度。

许多剂量反应曲线的标准斜率为 1.0。这种模型不假定标准斜率，而是根据数据拟合出 Hill 斜率，因此称为 变异性斜率 模型。在数据点较多的情况下，这种模型较为理想。它也叫四参数剂量反应曲线，或四参数逻辑曲线，简称 4PL。

步骤

创建 XY 数据表。在 X 中输入激动剂的浓度，在 Y 中以任何方便的单位输入反应。在 A 列输入一个数据集，必要时使用 B 列、C 列......输入不同的处理。

从数据表中点击分析，选择非线性回归，选择方程面板 "剂量反应曲线--激动剂"，然后选择方程"[激动剂] vs. 反应--变异性斜率"。

考虑将参数 HillSlope 限制为 1.0 的标准值。如果您的数据点不多，因此无法很好地拟合斜率，这一点尤其有用。

如果您已经减去了任何基底响应，则可以考虑将 Bottom 约束为 0 的恒定值。

由于 EC50 的不确定性非常不对称，请务必选择使用 似然比不对称法计算置信区间 。

双击图表的 X 轴，然后选择（在设置图表格式对话框的左上方）将轴拉伸为对数轴。

模型

Y=Bottom + (X^Hillslope)*(Top-Bottom)/(X^HillSlope + EC50^HillSlope)

 

解读参数

EC50 是在底面和顶面之间产生一半反应的激动剂浓度。这与 Y=50 时的反应不同。依赖于 Y 的表达单位以及 Bottom 和 Top 的值，EC50 可能会给出一个远低于 "50 "的反应。Prism 同时报告 EC50 及其对数。

HillSlope描述曲线族的陡度。HillSlope 为 1.0 是标准值，您应考虑将 Hill 斜率限制为 1.0 的恒定值。Hill斜率大于 1.0 表示陡峭，小于 1.0 表示较浅。

顶部 和 底部 是以 Y 轴为单位的高原。