什么是列常数？

当您同时拟合多个数据集时，可以将列标题作为第二个自变量。我们将此称为限制参数为列常数。本示例最能说明这一点。

如何输入列常数

要了解列常数的工作原理，请使用示例数据文件创建一个新的 XY 表：酶动力学 - 竞争性抑制。

数据表有一个 X 列和四个 Y 列，每个列代表不同浓度的抑制剂。抑制剂浓度作为列标题输入。

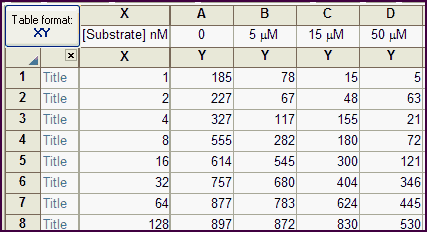
请注意，Prism 只读取列标题中的数字。在本示例中，单位指定为微摩尔，但 Prism 忽略了这一点，只读取数字。它不会进行任何单位转换。

拟合数据时指定列常数

选择初始值时，请从下拉列表中选择 "列标题平均值"或 "log(列标题平均值)"。

本示例

要拟合上述样本数据，请单击 "分析"（Analyze），选择非线性回归（Nonlinear regression），选择 "酶动力学"（Enzyme Kinetics）方程面板，然后选择 "竞争酶动力学"（Competitive enzyme kinetics）。方程已内置，但如果单击 "详细信息"按钮，就可以看到计算结果。

KmObs=Km(1+[I]/Ki)

Y=Vmax*X/(KmObs+X)

第一行定义了一个中间变异性变量（KmObs，存在竞争性抑制剂时观察到的迈克尔斯-门顿常数），它是酶的迈克尔斯-门顿常数（Km）、抑制剂浓度（I）和竞争性抑制常数（Ki）的函数。

第二行计算的酶速度（Y）是底物浓度（X）和 KMapp 的函数。

在定义该模型时，I 被限制为数据集常数，即其值来自列标题。因此，在本示例中，拟合 A 栏时 I=0，拟合 B 栏时 I=5，等等。Prism 会忽略标题中的 "μΜ"--它不会进行任何单位转换。

其他三个参数（Km、Ki 和 Vmax）被定义为共享参数，因此 Prism 拟合一个适用于整个数据集系列的拟合优度值。

Prism 确定了无抑制剂时酶的最大速度（Vmax，单位与您输入的 Y 值相同）、无抑制剂时酶的 Michaelis-Menten 常数（Km，单位与 X 值相同）和竞争性抑制常数（Ki，单位与 X 列常数相同）。请注意，I 并非拟合参数，而是采用您在列标题中输入的常数值。KmObs 不是拟合参数，而是用于定义模型的中间变异性变量。

了解有关竞争性酶抑制的更多信息。

总结。柱常数的优势

通过使用列常量和全局拟合（共享参数），本示例确定了一个参数（Ki），该参数的值无法通过任何一个数据集确定，只能通过研究数据集之间的关系来确定。