问题:未达到足够高浓度的结合等温线
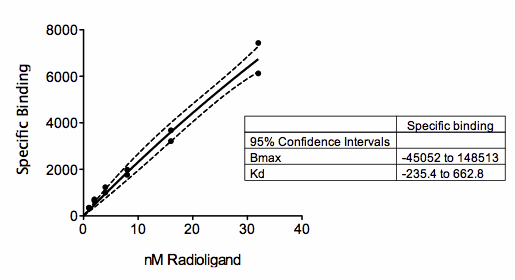
上图显示了与特异性结合数据拟合的饱和结合方程。但所有浓度都相对较低(与结合的 Kd 相比),因此数据几乎形成一条直线。饱和结合曲线模型很好地拟合了数据(实线),曲线周围有一个狭窄的 95% 置信带(虚线)。但请看 Bmax 和 Kd 的置信区间(如方框所示)!它们的置信区间超宽,甚至出现了负值(不可能)。对于这些数据,曲线拟合得很好,但模型中的两个参数(Bmax 和 Kd)都没有拟合出合理的置信区间。这并不奇怪。数据甚至没有显示出一丝高原现象,因此数据根本无法定义 Bmax 和 Kd。
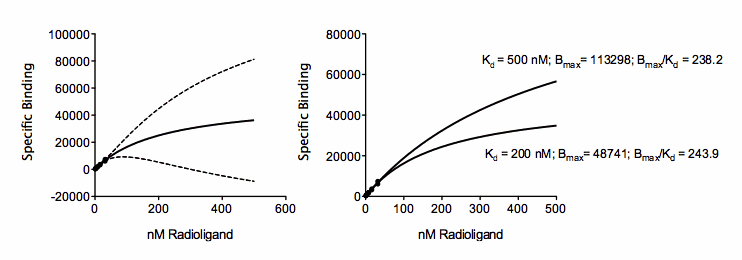
问题在于,这些数据与一个具有大量低亲和力受体(高 Bmax;高 Kd)或较少高亲和力受体(低 Bmax;低 Kd)的系统是一致的。下图展示了两种可视化方法。左图显示的拟合优度与上图相同,但最佳拟合曲线及其置信带延伸至更大浓度。虽然置信带在点附近很窄,但当它超出有数据的浓度时,置信带就会超宽。右图显示了两条不同的拟合曲线,Kd 分别为 200 nM 或 500 nM。曲线截然不同,但都接近数据。
看待这些数据问题的另一种方法是,Bmax 和 Kd 是相关的。Prism 可以报告协方差矩阵,作为非线性回归结果的一部分。由于只有两个参数,"矩阵"中只有一个值。Kd 和 Bmax 之间的协方差(范围从 0.0 到 1.0)为 0.9993。Prism 还可以报告每个参数的依赖度(范围也可以从 0.0 到 1.0)。在只有两个参数的情况下,两个参数的依赖度相同,本示例中的依赖度为 0.9986。这个依赖度还不够高,不足以让 Prism 宣布结果含糊不清,但这种指定的阈值(依赖度 > 0.9999)是任意设定的。
在这一点上,我们很容易放弃,认为如果没有更高浓度下的更多数据,就无法确定任何结果。但在某些系统中,尤其是使用 PET 扫描检测受体的系统中,这样的数据很典型。不可能使用更高浓度的配体。
拟合结合电位
从这些数据中可以了解到什么?数据几乎是线性的。这条线的斜率说明了什么?斜率,或者说初始斜率,被称为结合电位(1)。不要被 "势"这个词误导。它与势能和热力学无关。相反,它是对少量配体将发生多少结合的测量。
如果从特异性结合方程出发,求出它相对于 X(即浓度)的导数,并将 X 设为零,就可以得出特异性结合曲线的初始斜率。事实证明,这个斜率即结合力等于 Bmax/Kd。Bmax 的测量单位与数据中的 Y 值相同。Kd 的测量单位与 X 值相同。因此,结合电位的单位等于 Y 单位除以 X 单位。
Prism 可以拟合一条特异性结合曲线,还可以报告 Bmax/Kd 的比值及其置信区间。为此,您可以创建一个新的用户自定义方程,或者(更简单)克隆内置方程。然后转到定义方程对话框的最后一个选项卡。"报告变换"。选择报告两个参数的比值,并定义分子和分母。

在本示例中,Prism 发现结合电位为 242.1,置信区间为 183.4 至 300.7。置信区间相当窄,因此结果非常有用。
参考文献
1. Innis等:《可逆结合放射性配体体内成像的共识命名法》。脑血流与代谢杂志》(2007 年)第 27 卷(9)第 1533-1539 页