比较模式的方法

哪种模式 "最好"？起初，答案似乎很简单。非线性回归的目标是最小化平方和，因此平方和较小的模型显然拟合优度最高。但这也太简单了。

参数较少的模型对数据的拟合效果几乎总是较差。当您比较两个模型时，较简单的模型（参数较少）将具有较高的平方和。当您比较数据集时，整体拟合的平方和会高于单个拟合的平方和。当您比较有参数约束和无参数约束的拟合值时，将比无参数约束的模型具有更高的平方和。

F 检验和 AIC 方法既考虑了拟合优度的差异，也考虑了参数的数量。问题是平方和的减少（从简单模型到复杂模型）是否值得为拟合更多参数而付出的 "代价"。F 检验和 AICc 方法以不同的方式处理这个问题。

Prism 如何报告模型比较

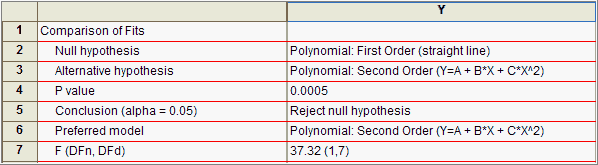
Prism 在非线性回归结果表的顶部报告比较结果。它清楚地说明了零假设和备择假设。如果您选择 F 检验，它会报告 F 比值和 P 值。如果您选择了 Akaike 方法，它会报告 AICc 的差异以及每个模型正确的概率。

最后，Prism 会报告 "首选"模型。您应该了解 Prism 如何决定哪个模型是 "首选"模型，因为您可能 "首选"另一个模型。

如果您选择了额外的平方和 F 检验，那么 Prism 会计算出一个 P 值来回答这个问题：

如果零假设真的正确，那么在多大比例的实验中（您的实验比例），平方和的差异会和您观察到的一样大或更大？

在 "比较"选项卡中，您还可以告诉 Prism 使用哪个 P 值作为截止值（默认值为 0.05）。如果 P 值小于该值，Prism 就会选择更复杂的模型。否则，它会选择更简单的模型。

如果选择 Akaike 修正方法，Prism 会选择更有可能正确的模型。但您应该看看这两个概率。如果它们的值相近，那么证据就没有说服力，两个模型都拟合得相当好。

比较模型的分析清单

两个模型都能拟合吗？

在运行额外的平方和 F 检验或计算 AICc 值之前，Prism 首先会做一些常识性的比较。如果 Prism 无法拟合任一模型，或者任一拟合模糊或完美，那么 Prism 不会对模型进行比较。

两个拟合都合理吗？

在接受 Prism 的结果之前，先进行现实检查。如果其中一个拟合结果在科学上无效，那么无论 F 检验或 AIC 比较的结果如何，都应接受另一个模型。

例如，如果其中一个阶段的幅度只占总响应的很小一部分，那么你就不会接受一个两阶段指数模型（尤其是在数据点不多的情况下）。如果其中一个阶段的半衰期值远小于第一个时间点或远远超过最后一个时间点，您也不会接受该模型。

首选模型的分析清单

在接受 "首选"模型之前，您应该考虑与只拟合一个模型时相同的一系列问题。您可以参考下面的详细核对表或缩略版。

拟合优度参数值的精确度如何？

置信带是否 "太宽"？

残差图好看吗？

拟合优度曲线周围点的散布是否服从高斯分布？