当 X 值为浓度或剂量时，使用该方程。当 X 值是浓度或剂量的对数时，使用相关方程。

引言

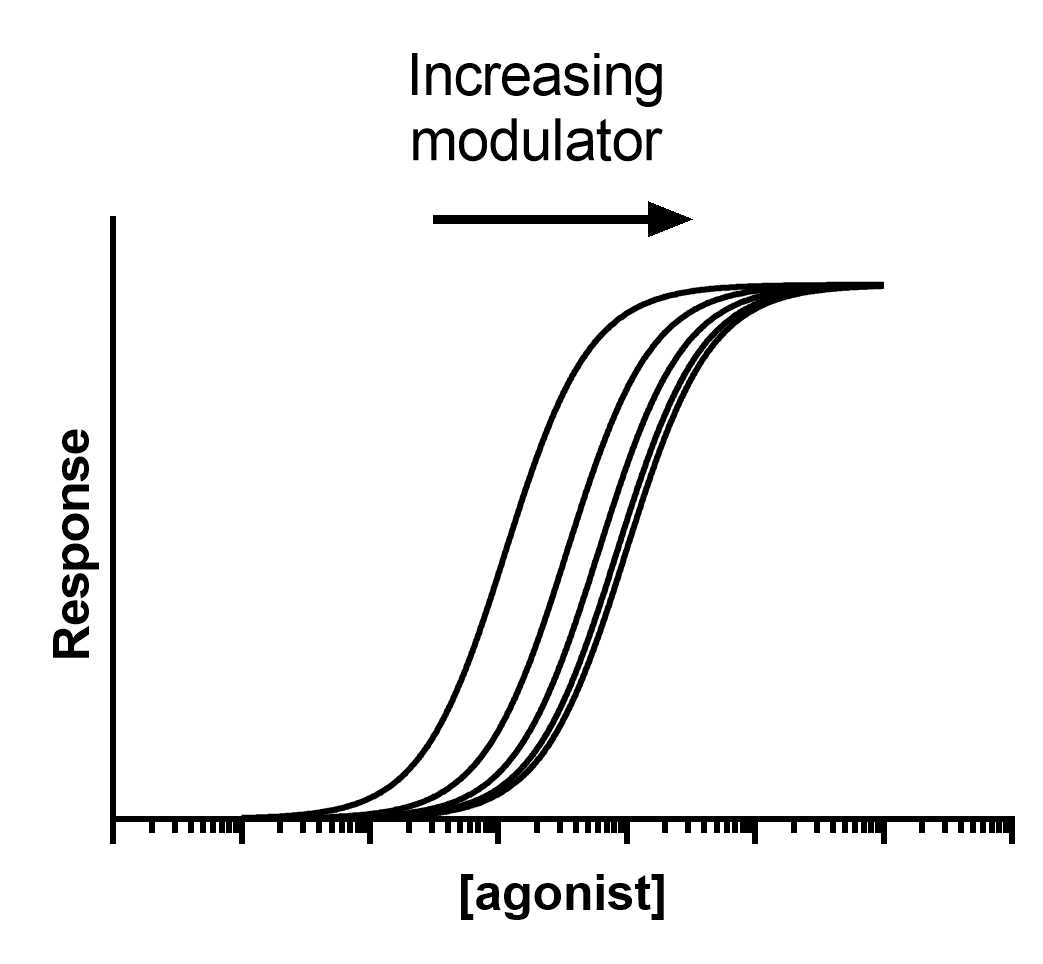
别构调节剂可以减少或增强激动剂的结合。该模型拟合了在没有调节剂和有调节剂的情况下测定的整个剂量反应曲线。其目的是了解调节剂与其受体位点结合的亲和力，同时确定三元复合物常数 alpha 的值，该常数可量化调节剂的结合改变放射性配体与受体位点亲和力的程度。

步骤

1.创建 XY 数据表。

2.如果浓度为 1nM，则输入 1e-9。

3.在 Y 中输入反应，单位不限。在 A 栏输入不含调节剂的数据，在 B 栏输入以恒定浓度调节剂收集的数据。如果有数据，重复 C、D、E...列，每列使用不同浓度的调节剂。

4.在列标题中输入调节剂浓度（以摩尔为单位，因此 1nM 输入 "1e-9"）。别忘了输入 "0"作为数据集 A 的列标题。您输入的值将成为分析的一部分。

5.在数据表中单击分析，选择非线性回归，然后选择方程组： 剂量-反应-特殊，X 为浓度。然后选择Allosteric EC50 shift，X 为浓度。

您无需将任何参数限制为恒定值

模型

Antag=(1+B/KB)/(1+α*B/KB)

Y=Bottom+(Top-Bottom)/(1+(EC50*Antag/X)^HillSlope)

 

logEC50 和 EC50 分别是 在没有调节剂的情况下产生半数最大反应的激动剂浓度和激动剂浓度的对数。请注意，虽然每条拟合曲线都有各自的 EC50，但 Prism 拟合并报告的参数是激动剂在无调节剂时的 EC50。

KB是调节剂与其别构调节位点结合的平衡解离常数（摩尔）。其摩尔单位与在数据表标题栏中输入调节剂浓度时使用的单位相同。

Alpha 是 三元复合常数。当 Alpha=1.0 时，调节剂不会改变结合。如果 Alpha 小于 1.0，则调节剂会减少配体的结合。如果 Alpha 大于 1.0，则调节剂会增加结合力。在本示例中，Alpha 等于 0.01，因此调节剂大大降低了结合力。

顶部 和 底部 是以 Y 轴为单位的高原。

注释

•该模型旨在分析调节剂通过别构调节剂发挥作用时的数据。由于激动剂和调节剂通过不同的位点起作用，因此将调节剂称为竞争者是不正确的。

•编写模型是为了拟合 alpha 本身，而不是 alpha 的对数。然而，α 是不对称的：所有从 0 到 1 的值都意味着调节剂会降低结合力，而所有从 1 到无穷大的值都意味着调节剂会增强结合力。在对数标度上，其值更加对称，因此按对数标度计算的置信区间（如 Prism 所做的）更加准确。Prism 同时报告 alpha 和 log(alpha)。

•该模型假定别构调节剂过量存在，因此您添加的浓度与其游离浓度非常接近。当别构调节剂的浓度受到限制时（如 G 蛋白改变激动剂与许多受体的结合时），该模型就不起作用了。任何显式模型都无法处理这种情况。您需要用隐式方程（Y 在等号两边）定义模型，而 Prism 无法处理此类方程。

•请注意，随着别构调节剂浓度的增加，曲线从左到右的发展有两个要点。首先，请注意最大反应没有变化。其次，注意调节剂使剂量反应曲线右移的效果在调节剂饱和其结合位点时达到最大值。

参考文献                                                                          

A.Christopoulos 和 T. Kenakin, Pharmacol Rev, 54: 323-374, 2002