在用线性回归分析数据之前，先停下来问问自己，用非线性回归拟合数据是否更有意义。如果您对非线性数据进行了转换以创建线性关系，那么几乎可以肯定的是，使用非线性回归拟合原始数据会更好。

在非线性回归出现之前，分析非线性数据的最佳方法是转换数据以创建线性图形，然后用线性回归分析转换后的数据。本示例包括酶动力学数据的 Lineweaver-Burk 图、结合力数据的 Scatchard 图和动力学数据的对数图。

这些方法已经过时，不应再用来分析数据。

这些方法的问题在于转换会扭曲实验误差。线性回归假设直线周围的点的散布服从高斯分布，并且在 X 的每个值上标准偏差都相同。这些假设在变换数据后很少能成立。此外，有些变换会改变 X 和 Y 之间的关系。例如，在 Scatchard 图中，X 的值（约束）被用来计算 Y（约束/自由），这就违反了线性回归的假设，即所有的不确定性都在 Y 中，而 X 是精确已知的。如果 X 和 Y 方向都出现相同的实验误差，那么最小化各点与直线垂直距离的平方和是没有意义的。

由于违反了线性回归的假设，从回归线的斜率和截距得出的值并不是模型中变量最精确的确定值。考虑到您为收集数据所花费的时间和精力，您希望使用尽可能好的技术来分析数据。非线性回归能得出最准确的结果。

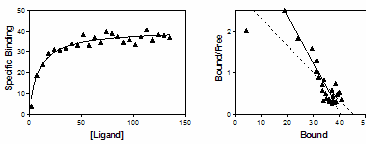
下图显示了数据转换问题。左侧面板显示的是遵循直角双曲线（结合等温线）的数据。右图是相同数据的 Scatchard 图。左边的实线曲线是通过非线性回归确定的。右边的实线显示了同一曲线在经过斯卡查德变换后的效果。虚线表示对转换后的数据进行线性回归拟合。斯卡查德图可用来确定受体数（Bmax，根据线性回归线的 X 截距确定）和解离常数（Kd，根据斜率的负倒数确定）。由于斯卡恰变换放大并扭曲了散点，因此线性回归拟合并不能得出最准确的Bmax和Kd 值。

不要为了避免使用非线性回归而使用线性回归。用非线性回归拟合曲线并不困难。

虽然分析转换后的数据通常并不合适，但显示线性变换后的数据往往很有帮助。很多人发现，直观地解读变换后的数据更容易。这是有道理的，因为人眼和大脑的进化是为了检测边缘（线）--而不是检测直角双曲线或指数衰减曲线。即使您使用非线性回归分析数据，显示线性变换的结果也是有意义的。