更简单

•插入值更容易。很多人使用非线性回归的目的是从标准曲线插入值。如果这是您的目标，那么非线性回归对话框中提供的大多数选项既不是必需的，也没有帮助。 Prism 6 只为插入曲线值提供了一种新的分析方法。它只提供基本选项，因此使用起来非常简单。

•绘制函数图，了解函数。在使用方程作为数据拟合模型之前，最好先了解它。一个很好的方法就是绘制函数图，看看在改变参数时函数是如何变化的。Prism 使用名为生成曲线族的分析方法绘制函数图。除了（或代替）绘制函数本身之外，Prism 6 现在还可以绘制函数的一阶导数、二阶导数及其积分。

用非线性回归拟合更多类型的模型

•隐式方程和微分方程。用代数和微积分来表达一个模型，并将 Y 定义为 X 和参数的函数，这并不是一件有趣的事情。这甚至是不可能的。不如将模型表示为微分方程（输入定义 dY/dX 的方程）或隐式方程（Y 出现在等号两边的方程）。

•编写更复杂的模型。 Prism 通过指定方程中的某些线段只适用于特定的数据集，5 可以让您为不同的数据集定义不同的模型。例如，等式中以 <B> 为前的一行只适用于数据集 B。Prism 6 扩展了这一语法，允许使用更复杂的等式。在一行前面加上 <A:D>，使其只适用于 A-D 列，或加上 <A:K,2>，使其适用于 A 和 K 之间的每第二个数据集（A、C、E、G、I、K）。

•新的加权选择。在使用非线性回归拟合数据模型时，对数据进行适当加权非常重要。Prism 总是提供多种权重选择。 Prism 在非线性回归对话框的加权选项卡中，K 是您输入的常数。

 

非线性回归的其他结果

•霍加偏斜度。使用非线性回归拟合数据时，可以选择多种方式表达参数。例如，可以选择拟合速率常数或半衰期。霍加德偏斜度量法可以帮助您选择不确定性更接近对称区间的参数化，这样置信区间会更准确。

•调整后R2。 Prism 报告调整后的R2，它考虑了自由度的数量，因此可以在参数数量不同的模型之间进行比较。

线性回归

•一键将线性回归转换为非线性回归。线性回归可以看作是非线性回归的一个特例。Prism非线性回归分析可用于拟合直线，有十多种理由可以解释为什么要这样做。但很少有人会想到用非线性回归分析来拟合直线。 Prism 6 使切换变得更容易--只需单击线性回归对话框上的 "更多选择 "按钮。

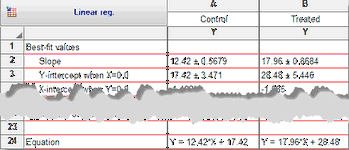
•复制线性回归方程。Prism 总是报告斜率和截距的拟合优度值，但不是以方程的形式。 Prism 6 现在可以报告线性回归方程，随时可以复制并粘贴到图表或手稿中。