常用方法会导致误导性结果

这种方法很诱人，但却是错误的（所以划掉了）：

与其在开始研究前选择样本量，不如在收集更多数据时简单地重复统计分析，然后：

•如果结果在统计学上不显著，再收集一些数据，然后重新分析。

•如果结果在统计学上显著，则停止研究。

这种方法的问题在于，如果你不喜欢结果，你就会继续研究，但如果你喜欢结果，你就会停止研究。这样做的后果是，如果零假设成立，得到 "显著"结果的几率要比 5%高得多。

模拟演示问题

下图通过模拟说明了这一点。我们通过从高斯分布（均值=40，SD=15，但这些值是任意的）中抽取数值来模拟数据。两组都使用完全相同的分布进行模拟。我们在每组中挑选 N=5，计算非配对 t 检验并记录 P 值。然后，我们在每组中增加一名受试者（因此 N=6），并重新计算 t 检验值和 P 值。如此反复，直到每组的受试者人数达到 100 人。然后，我们将整个模拟重复三次。这些模拟是在两组组平均值完全相同的情况下进行的。因此，我们得到的任何 "统计学显著 "结果都一定是巧合--第一类错误。

该图将 Y 轴上的 P 值与 X 轴上的样本量（每组）对比。图表底部的绿色阴影区域表示 P 值小于 0.05，因此被视为 "统计学显著"。

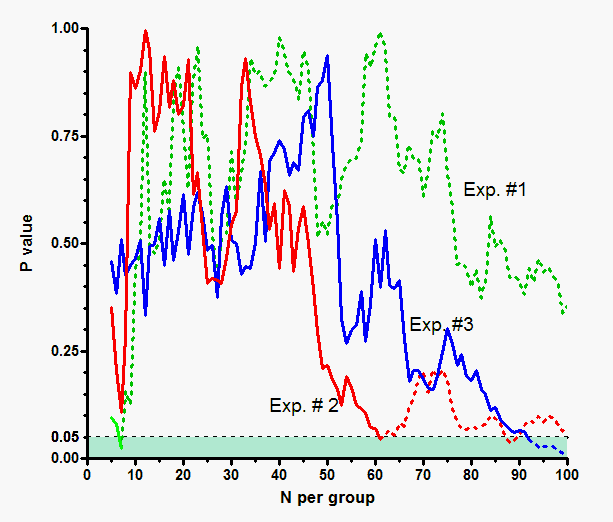
实验 1（绿色）在样本量为 7 时，P 值小于 0.05，但在其他样本量时，P 值均大于 0.05。实验 2（红色）在 N=61 时，P 值小于 0.05；在 N=88 或 89 时，P 值也小于 0.05。实验 3（蓝色）曲线在 N=92 到 N=100 时，P 值小于 0.05。

如果我们按照顺序进行实验，我们就会宣布这三个实验的结果都具有 "统计学显著性"。在第一个（绿色）实验中，我们会在 N=7 时停止实验，因此不会看到曲线的虚线部分。第二个（红色）实验在 N=6 时停止，第三个（蓝色）实验在 N=92 时停止。在这三种情况下，我们都会宣布实验结果 "统计学显著"。

由于这些模拟是针对两组真实平均值相同的值创建的，因此任何 "统计学显著性 "的声明都是 I 类错误。如果零假设成立（两组群体均值相同），我们期望在 5%的实验中看到这种 I 类错误（如果我们使用传统的 alpha=0.05 定义，那么 P 值小于 0.05 就会被宣布为显著）。但采用这种顺序方法，我们的三个实验都出现了I 类错误。如果你把实验时间延长得足够长（无限 N），所有实验最终都会达到统计学显著性。当然，在某些情况下，即使没有 "统计学显著性"，你最终也会放弃。但是，即使零假设为真，这种有序的方法也会在远超 5%的实验中产生 "显著"结果，因此这种方法是无效的。

小结

选择样本量并坚持下去非常重要。如果你喜欢的结果就停下来，不喜欢的结果就继续下去，你会自欺欺人。另一种方法是使用专门的顺序或适应性方法，这种方法会考虑到你在分析数据的过程中这一事实。要了解这些技术的更多信息，请在高级统计学书籍中查找 "序列"或 "自适应"方法。