几何均值的关键信息

•Prism 计算几何平均数的方法是先计算所有数值的对数，然后计算对数的平均数，最后取反对数。

•Prism 使用以 10 为底（常用）的对数，然后将对数的平均值取 10 的幂，得到几何平均数。有些程序使用自然对数，然后使用指数函数转换回来。

•使用对数和反比例相当于将所有数值相乘，然后将乘积取 1/n 的幂，其中 n 是数值的个数。你会在一些书中看到这个定义。

•如果有数值为零或负数，则无法计算几何均值。

•几何均值的单位与数据和算术均值相同。

•几何均值永远不会大于算术均值。

•如果数据是从对数正态分布中采样的，几何均值可能是表示分布中心的最佳方法。

几何 SD 因子

当您请求几何平均数时，Prism（在 Prism 7 中引入）会报告几何均值因子。它还可以在某些图形上绘制几何均值及其几何自变量因子。

关于几何自整数因子的主要事实：

•几何自变量一词并不常用。它是由 Kirkwood (1) 提出的。

•如何计算几何自整数：首先，将所有数值转换为对数，计算这些对数值的样本自差，然后求出自差的对数。

•几何 SD 因数没有单位。它是一个无单位的比率。它还必须大于或等于 1（只有在所有数据完全相同的情况下才会等于 1，这意味着数据对数的标准偏差为零，因为零的对数是 1）。

•你不能把几何标准差加到几何均值（或任何其他值）上，从几何均值中减去几何标准差也同样毫无意义。几何自变量是一个可以乘以或除以的值。这与普通标差截然不同，普通标差的单位与数据相同，因此可以与均值相加或相减。

•如果数据是从对数正态分布中采样的，那么从（几何均值除以几何标差因子）到（几何均值乘以几何标差因子）的范围将包含约三分之二的数值。同样，如果数据是从高斯分布中采样，从（均值减去标差）到（均值加上标差）的范围将包含约三分之二的数值。

•很少有出版物显示几何标差。常见的情况是报告结果为 "平均值为 3.2 ± 1.2 (SD)"。但目前很少有报告称几何均值为 4.3*?1.14。我输入的不是 "加或减 "符号，而是 "乘或除以"符号。

•虽然用 "乘以或除以"来表示误差似乎有些奇怪，但实际上它并不比 "加或减"陌生。

本示例

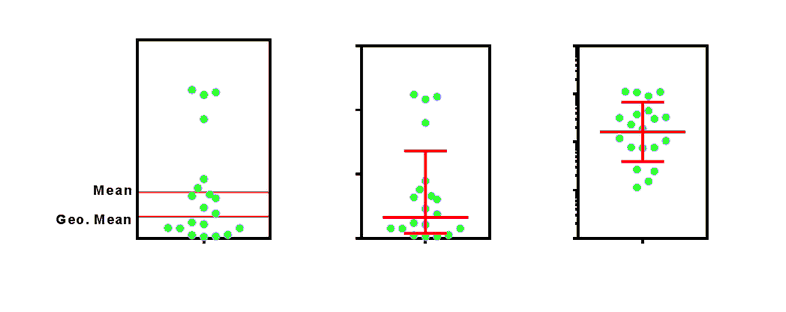
上图是从对数正态性分布中取样的 20 个数值。左图告诉你，均值和几何均值有很大不同。中间的图形绘制的是几何均值，误差条形图的计算方法是几何均值乘以或除以几何自变量系数。该图以对数 Y 轴显示同样的内容。现在的分布看起来是对称的，误差条似乎在每个方向上都延伸了相同的距离。但在中间和右边的图形中，误差条的两端处于相同的 Y 值。右图使用的是对数轴。

参考

1.Kirkwood, TBL (1979). "Geometric means and measures of dispersion".Biometrics 35: 908-9.