一次Prism分析可平滑曲线和/或将曲线转换为导数或积分。
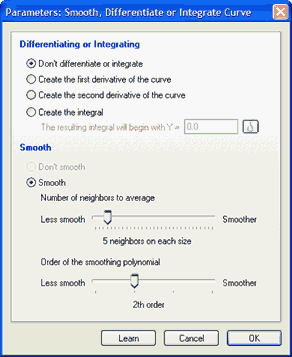
求曲线的导数或积分
一阶导数是曲线在每个 X 值处的陡度。曲线上坡时导数为正,曲线下坡时导数为负。在曲线的波峰和波谷处,导数等于零。计算数值导数后,Prism 可以对结果进行平滑处理。
二阶导数是导数曲线的导数。二阶导数在曲线拐点处等于零。
积分是曲线与 Y=0 处直线或您输入的其他值之间的累积面积。
注意
•Prism 不能进行符号代数或微积分运算。如果给 Prism 一系列定义曲线的 XY 点,它可以根据这一系列点计算数值导数(或积分)。但是,如果给 Prism 一个方程,它就无法计算出定义导数或积分的新方程。
•该分析对曲线进行积分,从而得到另一条显示累积面积的曲线。不要与计算曲线下面积单一值的单独 Prism 分析混淆。
平滑曲线
如果从仪器导入曲线,可能需要平滑数据以改善图表的外观。由于平滑曲线会丢失数据,因此在进行非线性回归或其他分析之前不应平滑曲线。
Prism 提供了两种调整曲线平滑度的方法。您可以选择要平均的相邻点的数量和平滑多项式的 "阶数"。由于平滑的唯一目的是让曲线看起来更好看,因此您只需尝试几种设置,直到您喜欢结果的外观为止。如果设置过高,会丢失一些峰值,而这些峰值会被平滑掉。如果设置过低,则曲线不够平滑。正确的平衡是受试者的主观意愿决定的--请多试错法。
结果表的行数要少于原始数据。
不要分析平滑数据
平滑曲线可能会产生误导。我们的目的是减少 "模糊",以便看到实际趋势。问题是,你可以看到实际上并不存在的 "趋势"。下面上排的三张图是模拟数据。每个值都取自均值为 50、标准偏差为 10 的高斯分布。每个值都是从该分布中独立抽取的,与之前的值无关。观察这三幅图,你会看到水平线周围的随机散点,这正是数据的生成过程。
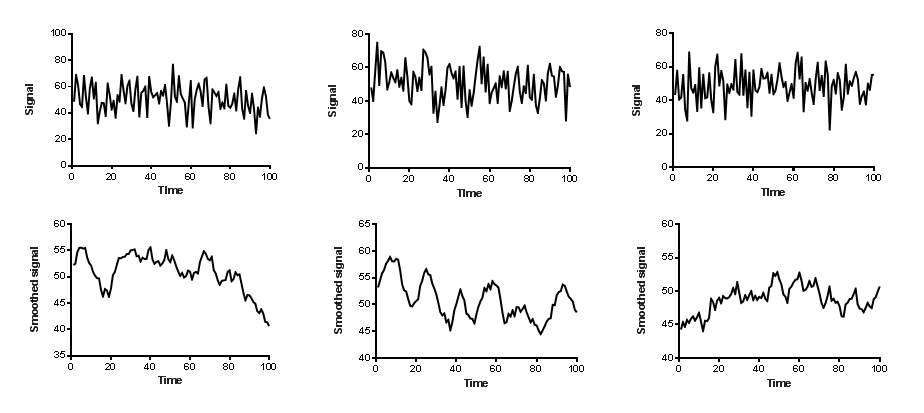
上面最下面的三张图显示了平滑后的相同数据(每边平均 10 个值,使用二阶平滑多项式)。观察这些图表,你会发现趋势。第一张图呈下降趋势。第二个图表似乎有规律地摆动。第三个图表趋于上升。所有这些趋势都是平滑的结果。每个图表显示的数据都与上一个图表相同。
对数据进行平滑处理,可以确保任何大幅随机变异性的高值或低值都会被放大,而点到点的变异性则会被弱化,从而给人造成趋势的印象。相关性、线性回归和非线性回归的一个关键假设是数据相互独立。对于平滑数据,这一假设并不成立。如果某个值碰巧超高或超低,那么平滑后的邻近点也会超高或超低。由于随机趋势被放大,随机散点被弱化,因此任何对平滑数据的分析(不考虑平滑因素)都是无效的。
数学细节
•一阶导数的计算方法如下(x 和 Y 是数据数组;x' 和 y' 是包含结果的数组)。
x'[i] = (x[i+1] + x[i]) / 2
y' at x'[i] = (y[i+1] - y[i]) / (x[i+1] - x[i])
•二阶导数是通过运行该算法两次来计算的,本质上是计算一阶导数的一阶导数。
•Prism 使用 梯形法则 对曲线进行积分。结果的 X 值与分析数据的 X 值相同。结果的第一个 Y 值等于您指定的值(通常为 0.0)。对于其他行,得到的 Y 值等于前一个结果加上该点所增加的曲线面积。该面积等于 X 值之差乘以前一个 Y 值和这个 Y 值的平均值。
•平滑处理是通过 Savistsky 和 Golay (1) 方法完成的。
•如果要求 Prism 既平滑又转换为导数(一阶或二阶)或积分,Prism 会按顺序完成这些步骤。首先创建导数或积分,然后进行平滑处理。
参考
1.A. Savitzky and M.J.E. Golay, (1964).用简化最小二乘法程序平滑和微分数据》。Analytical Chemistry 36 (8):1627-1639