Prism 提供两种选择：

1.对称法是 Prism 4 及更早版本中提供的唯一方法，现在提供这种方法只是为了兼容。它使用格林伍德方法，我们不推荐使用。

2.非对称法更为精确，值得推荐。Machin (1) 第 42 和 43 页对此进行了解释。该书没有给出该方法的名称或参考文献，但其原理是首先进行变换（平方根和对数），使生存的不确定性接近高斯。然后计算标准误差和对称的 95% CI。最后，它将置信限反变换回原始标度

生存分析计算的是中位生存时间及其置信区间。这样做的原因是，一旦生存曲线下降超过 50%，即使许多受试者尚未经历相关事件，中位生存时间也已完全确定。而且，即使某些受试者的数据被删剪，中位生存时间也是确定的。

相比之下，平均存活时间在每个受试者都经历过相关事件之前根本无法确定。只有知道每个受试者的存活时间（即没有受试者被删剪），才能计算出这个值。这种情况只在少数研究中出现，因此 Prism 不会计算平均生存时间。

但有一个简单的解决方法。如果您知道每个受试者的生存时间，只需将其输入列表，然后执行描述性统计分析，即可计算出这组值的平均值和置信区间。

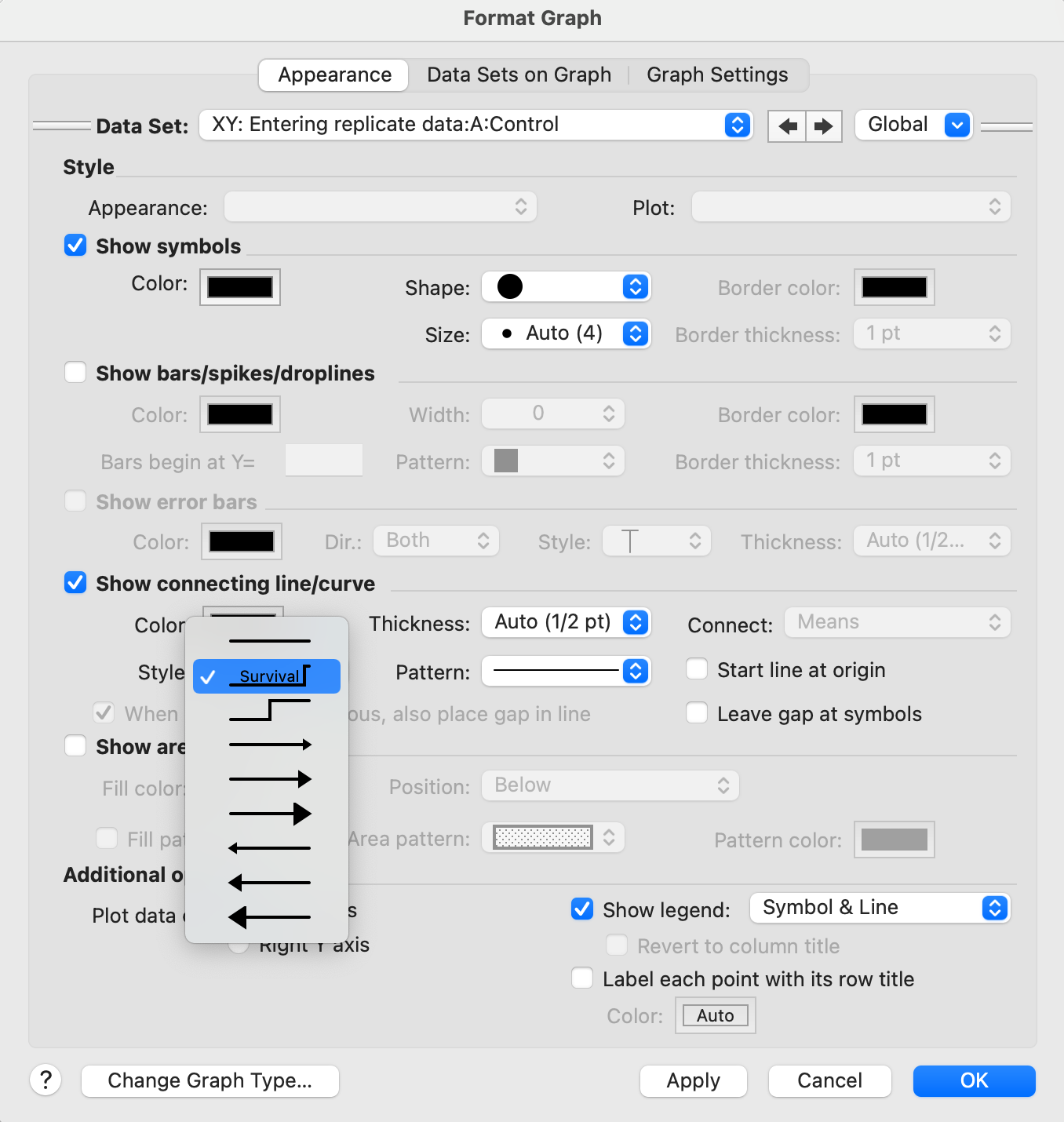
Prism 只能根据生存数据表中的原始数据创建Kaplan-Meier 生存曲线，并使用对数秩检验（或 Gehan-Breslow-Wilcoxon 检验）对这些曲线进行比较。

如果您已经知道每个时间点的存活概率，只想绘制图表，则不应将数据输入存活率数据表。相反，您可以创建一个 XY 数据表。将每个时间点输入 X 值（数字，而不是日期），并将这些时间点的相应生存概率输入 Y 值（不设子列）。如果您还想得到各时间点生存概率的标准误差信息，可以设置 XY 数据表格式，允许您在 Y 列的子列中输入该信息，设置数据表格式为 "输入并绘制已在其他地方计算出的误差值"，选项为 "带 SEM 的平均值"。

适当输入数据后，您就可以对生成的图形进行抛光。如果希望图表包含阶梯式曲线（生存曲线的传统样式），请打开设置图表格式对话框，在 "显示连接线/曲线 "部分的样式下拉菜单中选择生存曲线。

如果在 XY 表格中输入存活率，则无法进行存活率计算。您将无法计算误差条或置信带，也无法使用 Prism 提供的检验来比较生存曲线。

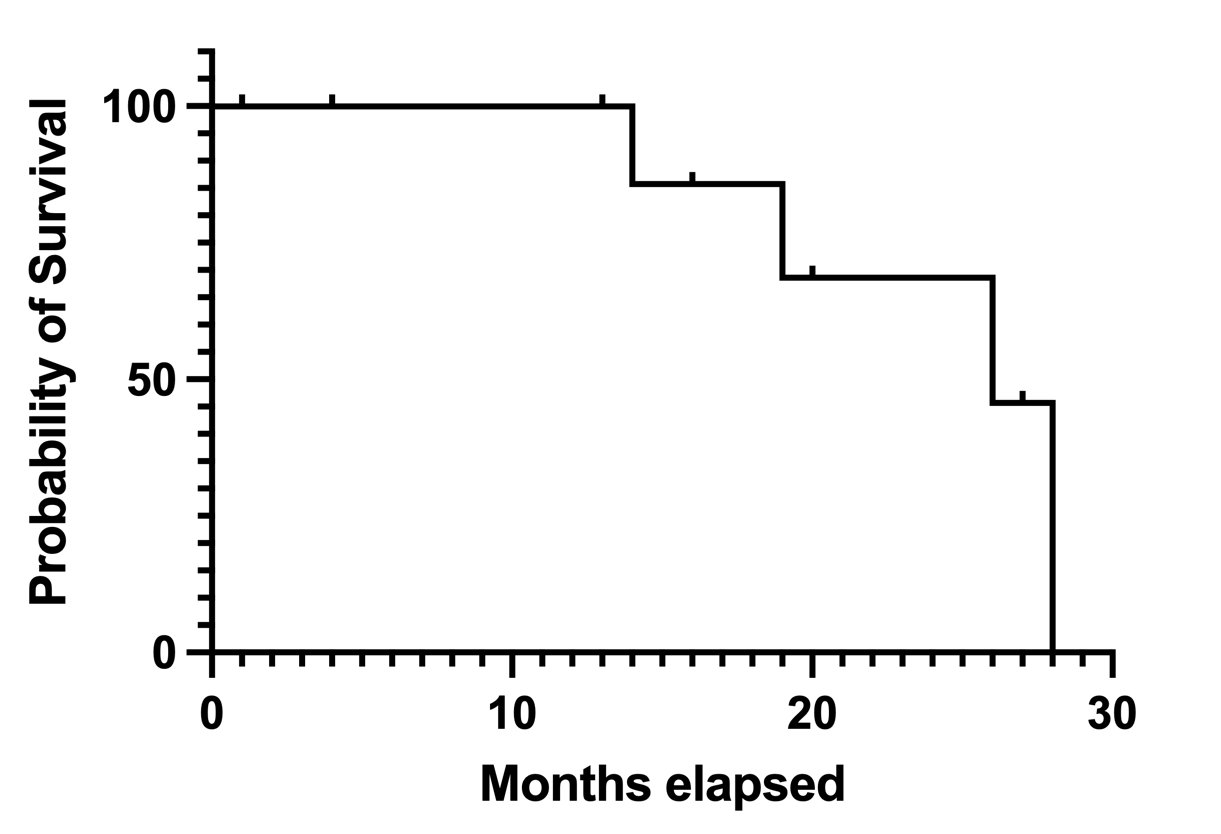
如果没有删剪观测值

如果跟踪每个受试者直到感兴趣的事件发生（事件通常是死亡，但生存曲线可以跟踪直到任何一次性事件发生的时间），那么曲线最终将到达 0。在最后一个受试者经历感兴趣事件的时间（X 值），生存概率将为零。

如果所有受试者的跟踪时间完全相同

如果所有受试者的跟踪时间相同，情况就很简单了。如果三分之一的受试者在研究结束时尚未经历相关事件，那么存活概率为 33%。

如果某些受试者在研究过程中被删剪

如果任何受试者的观测数据被删剪，那么生存曲线的底点将不等于研究结束时未经历相关事件的受试者比例。

在删剪之前，受试者对分数生存值有贡献。在此之后，受试者不会影响计算。在任何给定时间，存活概率值都是受试者在该时间段内存活的比例。

受试者的观察结果被删剪--要么因为他们离开了研究，要么因为研究结束了--在删剪时间之后就不能再贡献任何信息了。你不知道他们在删剪后是否会经历感兴趣的事件（或者你知道，但无法使用这些信息，因为实验方案不再被遵循）。因此，如果有受试者在生存曲线 X 轴上显示的最后一次时间之前被删剪，那么生存曲线图上显示的最终生存概率将不符合没有经历相关事件的受试者的实际比例。那个你可以很容易地用手计算出来的简单的存活率是没有意义的，因为并不是所有的受试者都没有被跟踪相同的时间。

生存曲线何时会降到零？

如果生存曲线一直下降到 0% 的生存率，这并不意味着研究中的每个受试者都经历了感兴趣的事件。有些受试者可能在较早的时间点就被删剪了（要么因为他们离开了研究，要么因为研究在他们经历相关事件之前就结束了）。当最后一个时间点的观察对象是经历了相关事件的受试者，而不是被删剪的受试者时，生存概率将降为零。如果您的数据按 X 值排序（Prism 可以使用编辑...排序），如果最后一个 Y 值为 1（感兴趣事件），曲线将下降到 0%的生存率；如果最后一个 Y 值为 0（删剪），曲线将在 0%以上结束。

在下面的本示例中，感兴趣的事件是死亡。10 名受试者中有 4 人死亡。但生存曲线下降到 0，而不是 60%。为什么呢？因为有六个受试者在 1 到 27 个月之间被删剪了。我们不知道如果他们在研究中坚持到第 28 个月会发生什么。因为我们不知道他们是生是死，所以他们的数据在删剪时间之后根本不算数（但在此之前肯定算数）。在第 27 个时间点，只有一名受试者仍在接受随访，她或他在第 28 个月死亡，存活概率降为零。

中位生存期是指达到 50%生存率所需的时间。如果超过 50%的受试者在研究结束时还活着，那么中位生存时间根本就没有定义。

P 值来自对数秩检验，它对整个曲线进行比较，即使生存概率总是大于 50%，也能正常工作。两条曲线可以有很大差异，即使它们的生存概率从未降低到 50%以下。

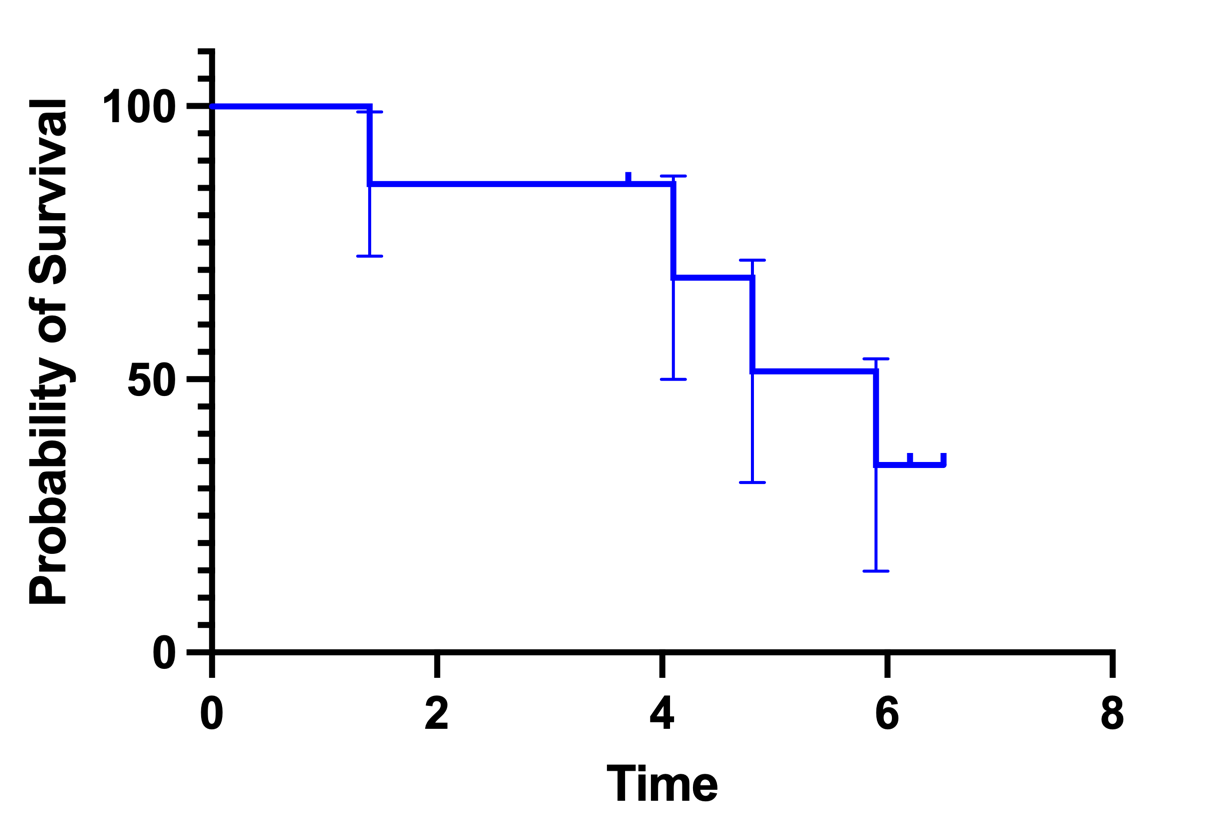
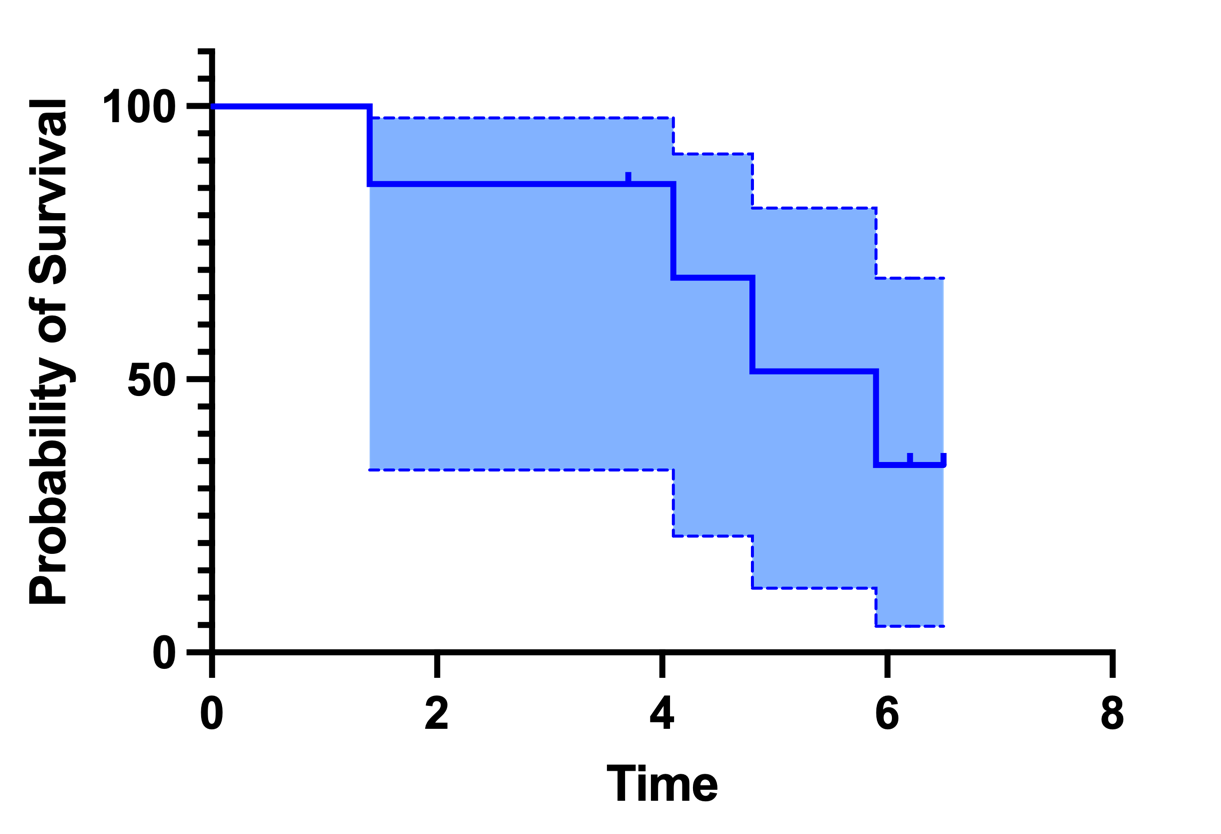
Prism 计算生存曲线时，还可以计算每个时间点的 95% 置信区间（使用两种可选方法）。这些方法都是近似方法，但可以像任何置信区间一样进行解读。您知道在研究的某个时间点上观察到的生存概率，并且可以 95% 地确信（给定一组假设）置信区间包含了真实的群体值（只有在对研究群体的每个成员都进行了观察的情况下，您才能确定这个值--如果研究的是人类，这就意味着存在的每个人）。

将这些置信区间绘制成误差条形图（如下左图）就没有问题了。Prism 还可以连接这些误差条形图的两端，并创建一个阴影区域（如下右图）。这条生存曲线绘制的是仅有 7 个个体的样本生存情况，因此置信区间非常宽。

阴影区域看起来就像线性和非线性回归计算出的置信带，因此很容易将这些区域解读为置信带。但是，说这些区域包含了整个生存曲线并不正确。正确的说法是，在任何时间点，您都可以 95% 地置信区间包含真实的生存概率。真实的生存曲线（你无法知道）在某些时间点可能在置信区间内，而在其他时间点可能在置信区间外。

计算生存曲线的真实置信带是可能的（不过，不是用 Prism），这些置信带比上图所示的置信区间更宽。换句话说，95% 确定包含所有时间点的整条生存曲线的置信带要比单个时间点的置信区间宽。

在分析生存数据时，Prism 会忽略任何 X=0 的行。如果替代疗法在时间零点开始，那么在治疗开始时死亡的患者无法提供任何信息来帮助您决定两种疗法中哪种更好。没有要求 X 必须是整数。如果死亡发生在治疗的半天后，而 X 值是以天为单位制表的，那么只需输入 0.5 作为该受试者的观察值即可。

有些领域（小儿白血病就是其中之一）认为时间为零的事件是有效的。这些研究不是简单地追踪死亡，而是追踪疾病复发前的时间。但疾病在缓解之前是不会复发的。在一些儿童白血病试验中，治疗是在时间零点前 30 天开始的。大多数患者在时间零点时病情得到缓解。然后对患者进行随访，直至死亡或疾病复发。但从未缓解的受试者怎么办？一些研究者认为这属于零时事件。有些方案将零时的事件考虑在内，因此Kaplan-Meier 生存曲线开始时的生存概率小于 100%。如果一个治疗组中有 10%的患者从未缓解，那么生存曲线的起点就是 Y=90%，而不是 100%。

由于以下原因，我们没有改变 Prism 以考虑零时发生的事件：

•我们没有看到任何科学论文和教科书解释分析零时死亡的意义。这似乎与标准相去甚远

•将两个截然不同的问题的答案合并到一条生存曲线中似乎是错误的：有多少患者病情得到缓解？缓解期的患者能维持多久？

•如果我们纳入 X=0 的数据，我们不能肯定生存分析的结果（生存时间中位数、风险比、P 值等）是否有意义

根本问题在于此：生存分析利用的数据是相关事件发生前的时间。这个事件通常是地球。通常情况下，它是其他一些定义明确的事件，每个受试者只能发生一次。此外，该事件的定义是--理论上--只要有足够的时间，试验中的每个参与者都可能发生。在这些小儿白血病试验中，事件被定义为疾病复发。当然，除非疾病首先得到缓解，否则不可能复发。因此，生存分析实际上是用来跟踪两个不同事件中第二个事件发生前的时间。这就引出了一个问题，即如何分析从未缓解（第一个事件从未发生）的患者的数据。

如果您认为我们的决定是错误的，请告诉我们。如果可能，请提供参考资料。

如果您真的想分析数据，那么有一个简单的变通方法，可以将零时的死亡人数将起点降至 100%以下。只需输入零以外的某个极小值即可。本示例中，输入这些值为 X=0.000001。另一种替代分析是输入 X=0 的数据，然后使用 Prism 的变换分析，并使用此用户自定义变换：

x=if(x=0, 0.000001, x)

在分析结果中，所有 X=0 的值都将转换为 X=0.000001。在该结果表中，单击分析并选择生存分析。

Prism 使用Kaplan-Meier 乘积极限法计算存活概率。这是一种标准方法。唯一的诀窍在于计算删剪观测值。

请看一个简单的本示例。一开始有 16 个个体。在 15 个月的第一次事件之前，有两个人被删剪。由于这两个人在第一次事件发生时不属于 "高危 "人群，因此在计算生存概率时不包括他们。因此，15 个月时的存活概率从 100%（16/16=100%）降至 92.86%（13/14=92.86%）。分母为 14 表明，剔除之前删剪的两人后，"高危 "人群中的人数只有 14 人。

在 93 个月的下一次事件之前，又有 7 人被删剪。因此，在存活超过 15 个月的人中，我们知道有 83.3%（5/6=83.3%）的人在 93 个月后还活着。但这只是相对下降。要知道在 0 个月时还活着的人在 93 个月后还活着的百分比，就必须用 92.86%（第一次事件发生时的存活百分比）乘以 83.3%（第二次事件发生时的存活百分比），得到 77.38%。这就是 Prism 报告的 93 个月时的存活概率。因此，Kaplan-Meier 方法也被称为乘积极限法。有关此方法的更多详情，请参阅本页。