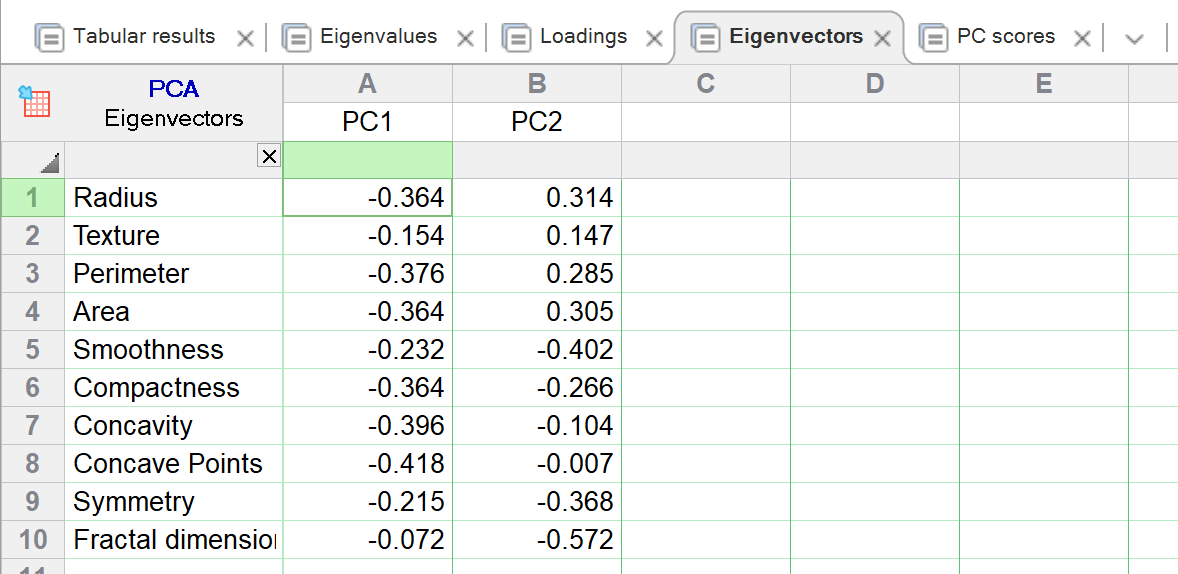
特征向量又称主成分向量，是变量的特异性线性组合。

在下面的本示例中：

•PC1 的定义是-0.364 * 半径 - 0.154 * 纹理 - 0.376 * 周长，以此类推

•PC2 定义为0.314 * 半径 + 0.147 * 纹理 + 0.285 * 周长，以此类推

特征向量是主成分分析（以及许多其他多元分析方法）的基础，因为它们定义了能解释输入数据中最大方差的向量。下表中的每列数值代表一个特征向量。特征向量仅显示所选选择方法选出的 PC 的特征向量。

请注意特征值和特征向量之间的区别。每个主成分的特征值都用一个值（一个数字）来表示，并量化了该成分对总体变异的解释程度。相比之下，每个主成分的特征向量对每个原始变量只有一个值（一个数字）。这些数字（如上所述）代表用于定义主成分的变量线性组合中的系数。

载荷、特征向量和特征值之间有什么关系？

是这样的载荷 = 特征向量 * sqrt（特征值）