有时您会读到，Mann-Whitney 检验比较两组的中位数。但正如本示例所示，这并不完全正确。

 

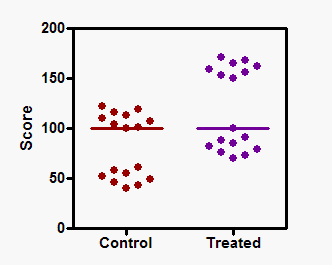
该图显示了从对照组和受试者身上得到的每个数值。通过 Mann-Whitney 检验得出的双尾 P 值为 0.0288，因此可以得出结论：两组之间存在统计学显著差异。但水平线所示的两个中位数是相同的。Mann-Whitney检验将所有值从低到高排序，然后比较平均等级。对照组数值的等级平均值远远低于治疗组数值的等级平均值，因此，尽管两组的中位数相同，但 P 值很小。

Mann-Whitney检验询问两组是否来自不同分布的人群，这种说法也不完全正确。下图中的两组显然来自不同的分布，但 Mann-Whitney 检验的 P 值却很高（0.46）。两组的标准偏差显然相差很大。但由于Mann-Whitney检验只分析等级，所以看不出组间有实质性差异。

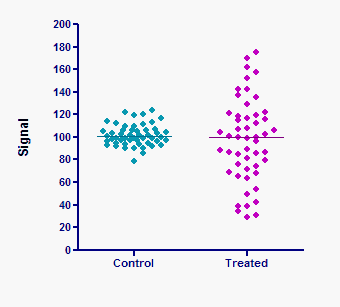
Mann-Whitney检验比较的是平均等级--它不比较中位数，也不比较分布。更一般地说，P 值可以回答这个问题：从平均等级较大的群体中随机选取的值大于从其他群体中随机选取的值的概率是多少？

如果再做一个假设--两个种群的分布形状相同，即使它们发生了偏移（具有不同的中位数）--那么曼-惠氏检验就可以被视为中位数检验。如果你接受分布形状相同的假设，那么Mann-Whitney检验得出的小 P 值就会让你得出结论：中位数之间的差异在统计学上显著。但 迈克尔-坎贝尔（Michael J. Campbell）指出："然而，如果各组具有相同的分布，那么位置的移动将使中位数和平均值移动相同的量，因此中位数的差异与平均值的差异相同。因此，Mann-Whitney 检验也是均值差异的检验"。

Kruskal-Wallis检验是比较三个或更多组的相应非参数检验。本页中有关 Mann-Whitney 检验的所有内容同样适用于 Kruskal-Wallis 检验。

1.A. 哈特Mann-Whitney检验不仅仅是中位数检验：散布差异可能很重要。BMJ (2001) vol. 323 (7309) pp.