P 值的可重复性比你想象的要低得多。

如果零假设为真，那么 P 值的分布就是均匀的。一半的 P 值小于 0.50，5% 的 P 值小于 0.05，等等。

但如果零假设是假的呢？大多数人会期望这种情况下的 P 值具有相当的可重复性。其实不然。

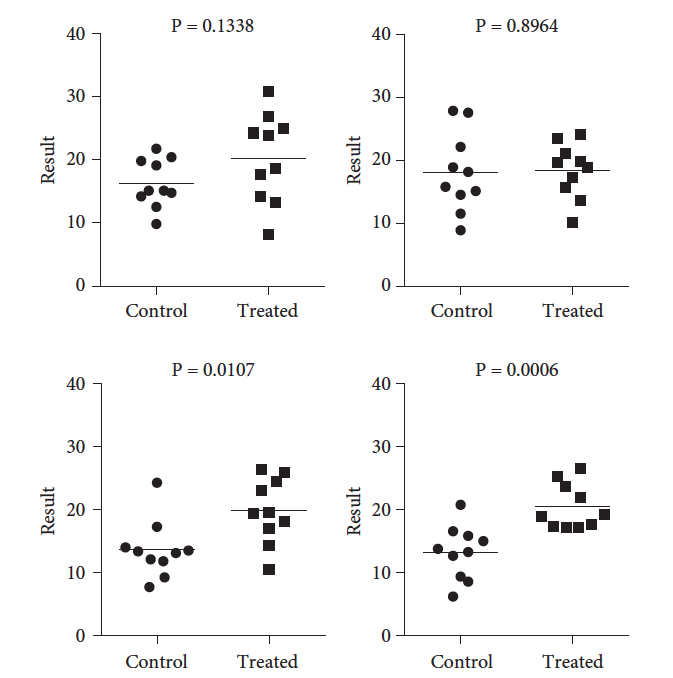
为了证明这一点，我使用 GraphPad Prism 进行了一些模拟。我从 SD 等于 5.0 的两个高斯群体中取样。两个群体的平均值相差 5.0。下面是四个模拟实验。四个实验之间仅有随机抽样。四个 P 值相差很大。

下面是 2500 次模拟实验的 P 值分布。X 轴绘制了不同的 P 值。Y 轴显示了该数值范围在 2500 次模拟实验中出现的频率。

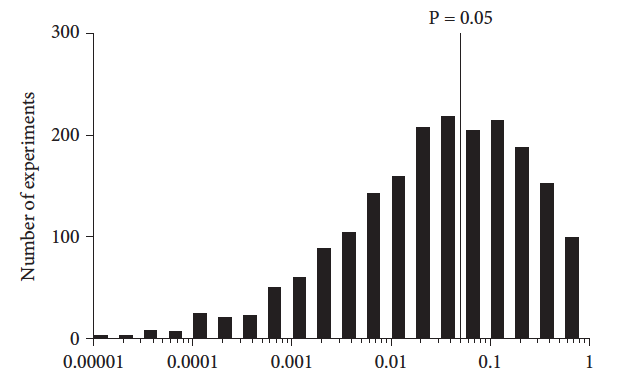
除去 2.5% 的最高 P 值和最低 P 值，中间 95% 的 P 值范围在 0.0001517 到 0.6869 之间，这个范围覆盖了三个数量级以上！

在这些模拟中，P 值的中位数约为 0.05。我还用较小的 SD 值进行了模拟，这当然会导致较小的 P 值，但范围仍然覆盖了三个数量级以上。

这些模拟的想法来自 Boos 和 Stefanski (1)，他们通过对一些情况的模拟证明，重复模拟实验的 P 值变化超过三个数量级。

Cumming (2) 问，如果一次特定实验的 P 值等于 0.05，那么重复实验的 P 值可能是多少（只考虑随机抽样，并假设两次实验都没有故障）。令人惊讶的是，结果并不依赖于样本量。当然，重复实验的 P 值大于 0.05 的概率为 50%。但令人惊讶的是（我认为），重复实验的 P 值大于 0.38 的概率为 20%，大于 0.82 的概率为 5%。

在分析数据时不依赖 P 值有很多原因。本页显示，除了避免使用 P 值的概念性原因外，还有一个非常实际的原因：P 值的可重复性不高。

上图是第三版《 直观生物统计学》中的图 15.1 。

 

1. Boos, D. D. & Stefanski, L. A.P 值精度与可重复性。The American Statistician 65, 213-221 (2011).

2. Cumming, G.Replication and p Intervals: P Values Predict the Future Only Vaguely, but Confidence Intervals Do Much Better.Perspectives on Psychological Science 3, 286-300 (2008).