引言

正弦波描述了许多振荡现象。

步骤

创建 XY 数据表。其中有一列 X 和一列或多列 Y。如果有多个实验条件，则将第一个实验条件放入 A 列，第二个实验条件放入 B 列，等等。

输入数据后，点击分析，选择非线性回归，选择正弦波的方程面板，然后选择标准正弦波。

如果知道 Y 值在零点时必须等于零，那么就将 PhaseShift 约束为一个恒定的零值。

您可能需要对 PhaseShift 和 Wavelength 的初始值进行调整，因为我们计算初始值的内置规则很少起作用。

•对于波长 计算两个值 X = a 和 X = b 之间的峰值数，并将波长的初始值设为 1/( 峰值数 / (b - a))。

•对于相移。如果 X=0 时 Y=0，则相移为零。如果 X=0 时 Y 为最大值，则相移=3.14159。必要时可在两者之间插入插值。

模型

Y= 振幅*sin((2*pi*X/波长)+相移)

 

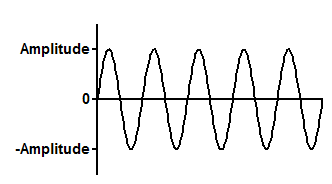
解读参数

振幅是波峰的高度，以 Y 为单位。如果 Prism 报告的振幅为负值，而您期望的振幅为正值，只需将相位偏移的初始值向任一方向改动 Pi 即可。

波长 是一个完整周期所需的时间，单位为 X

频率是每个时间单位的周期数。它是以波长的倒数来计算的，并以时间单位 X 的倒数来表示。

相位偏移（PhaseShift），单位为弧度。相移为 0 时，Y 等于 X=0 时的 0；相移为 pi 时，Y 等于 X=0 时的最大值。如果相移的拟合优度值让你感到惊讶，请记住正弦波是振荡的。你可以从相移中加上或减去 2*pi 来得到一个不同但等效的相移。调整初始值可以让 Prism 拟合出你想要的值。