与简单线性回归类似，简单逻辑回归也试图为一组参数找到拟合优度值。不过，与简单线性回归不同的是，简单逻辑回归是通过迭代程序找到拟合优度值的，该程序从这些参数的一些初始值开始，一步一步地找到拟合优度值。因此，对于某些数据集，这种迭代算法不可能计算出这些拟合优度值。出现这种情况时，Prism 会提供一条错误信息，指出数据中可能存在 "完美分离 "的问题，或者只有一个 X 值。

在确定拟合优度值的过程中涉及的数学概念（以及在此过程中可能出现的错误）对于简单逻辑回归和多元逻辑回归都是一样的。下面将对简单逻辑回归中可能出现此错误信息的原因进行非常基本的解释。关于模型拟合过程和可能出现的错误的更详细解释，请参阅多重逻辑回归的相应页面。

完美分离

分离是一个概念，适用于 X 变量的值可以完美预测 Y 变量的值时的数据集。换句话说，对于数据集中的每个观察值，当 X 小于某个值时，Y 将呈现一种结果，而当 X 大于该值时，Y 将呈现相反的结果。下面的数据就是一个完美分离的本示例：

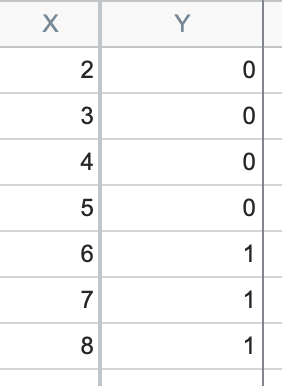
在上述数据集中，当 X 小于或等于 5 时，所有 Y 值均为 0，而当 X 大于 5 时，所有 Y 值均为 1。不可能拟合 S 形逻辑曲线，因为数据没有提供任何线索，说明当 X 为 5.1 或 5.5 或介于 5 和 6 之间的任何值时，期望值是多少。

当数据不是 "完美 "分离时，就会出现一个密切相关的问题，比如这个数据集：

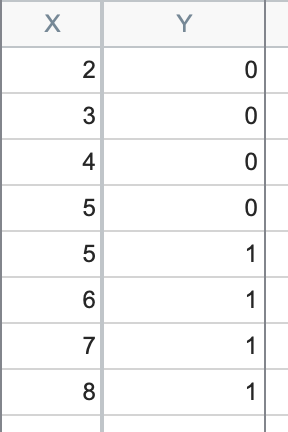
在这里，你可以看到，当 X 值小于 5 时，Y 值为 0，而当 X 值大于 5 时，Y 值为 1，但在 X = 5 时，我们同时观察到 Y = 0 和 Y = 1。这是一种特殊的分离情况，称为 "准完美分离"。

只有一个 X 值

简单逻辑回归的目标是根据预测因子（X 变异性）的值预测 "成功"（Y = 1）的概率。然而，如果您的所有观察值都具有相同的预测因子值，那么就不可能拟合出一个模型来预测 "成功 "概率与该预测因子的函数关系。

在数学上，这个问题是由β0 和 β1 之间的线性依赖度引起的。当模型有多个预测因子变量时，多元逻辑回归也会出现这个问题。