既然我们已经知道逻辑回归是如何使用几率对数将概率与系数联系起来的，那么我们就可以思考一下这些系数究竟在告诉我们什么。对于简单逻辑回归（和简单线性回归一样），有两个系数："截距"（β0）和 "斜率"（β1）。虽然您经常会看到这些系数被称为截距和斜率，但重要的是要记住，它们并不像简单线性回归中 X 和 Y 的对应系数那样，提供 X 和 P(Y=1)之间的图形关系。但它们能告诉我们什么呢？

•β0：当 X 变异性为 0 时的对数几率

•β1：当 X 变量增加（或减少）1.0 时，对数几率的变化程度

我们来看一个实际本示例。假设我们的简单逻辑回归模型为 Ln（几率）=-5.5 + 1.2*X。这里，β0 = -5.5，β1 = 1.2。这意味着当 X = 0 时，对数几率等于-5.5。这也告诉我们，X 每增加 1 个单位，对数几率就会增加 1.2（X 增加 2 个单位，对数几率就会增加 2.4，等等）。

不过，思考对数几率可能会令人困惑。因此，利用上述数学方法，我们可以重写简单逻辑回归模型，让它告诉我们几率（甚至概率）。

几率 =eβ0+β1*X

利用一些指数规则，我们可以得出

几率 = (eβ0)*(eβ1*X)

当 X 等于 0 时，第二项等于 1.0。因此，eβ0 就是 X 为零时的几率。在我们上面的本示例中，当 X 为零时，几率为 e-5.5，约为 0.009。此外，您还可以看到，X 每增加 1 个单位，几率就会乘以 eβ1。因此，如果 X 为 1，几率为 (e-5.5)*(e1.2) = 0.033。这些值（eβ0和eβ1）称为 "优势比"，由 Prism 报告简单逻辑回归。请注意，为清楚起见，Prism 简单地将优势比报告为 "β0 "和 "β1"，但从数值上看，它们实际上分别是eβ0和eβ1。

这些系数与 Y=1 的概率之间的关系式如下所示。不过，该方程中这些系数的解读比几率的解读更具挑战性，因此在此不一一列举。

P(Y=1) = (eβ0+β1*X)/(1+eβ0+β1*X)

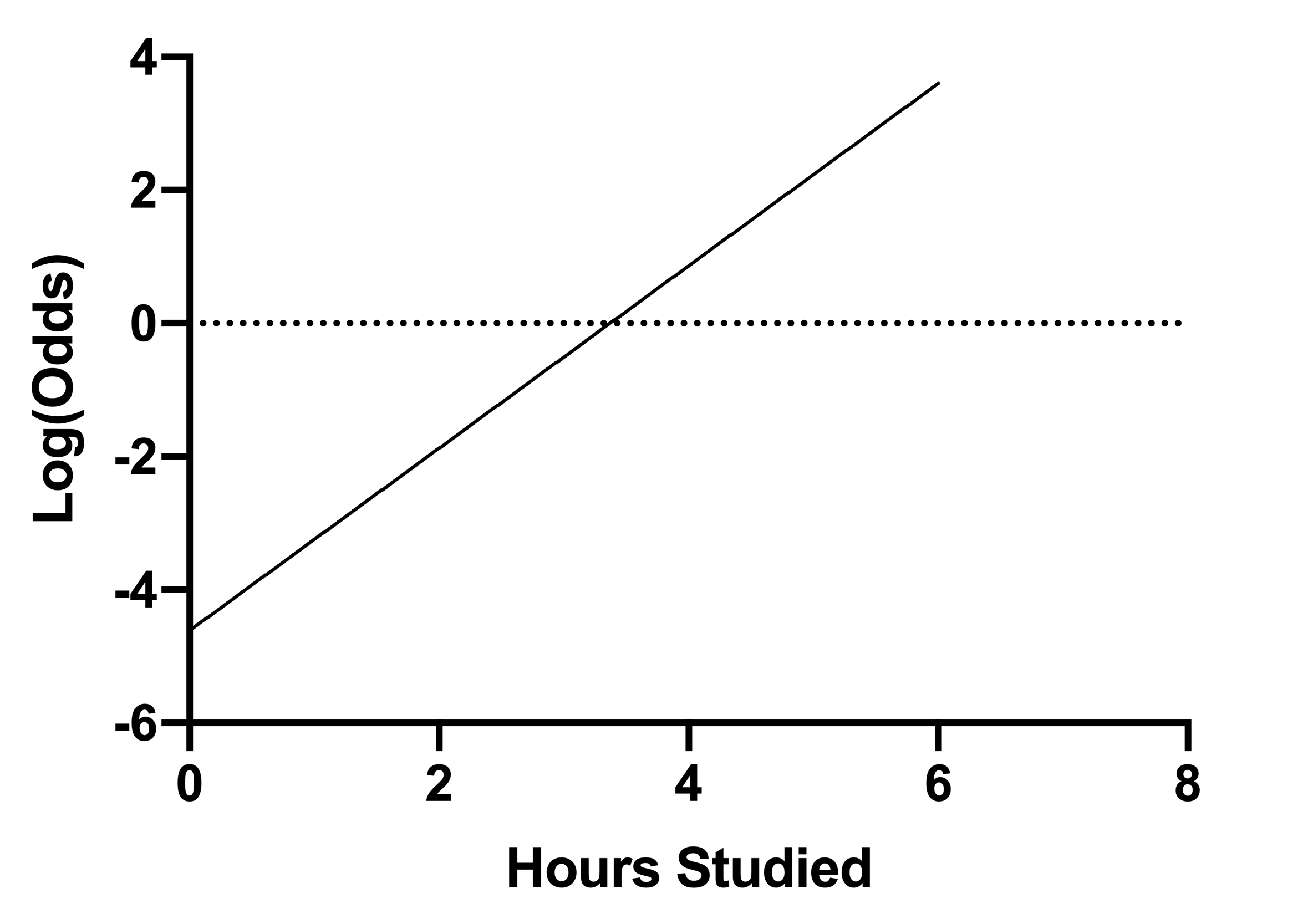
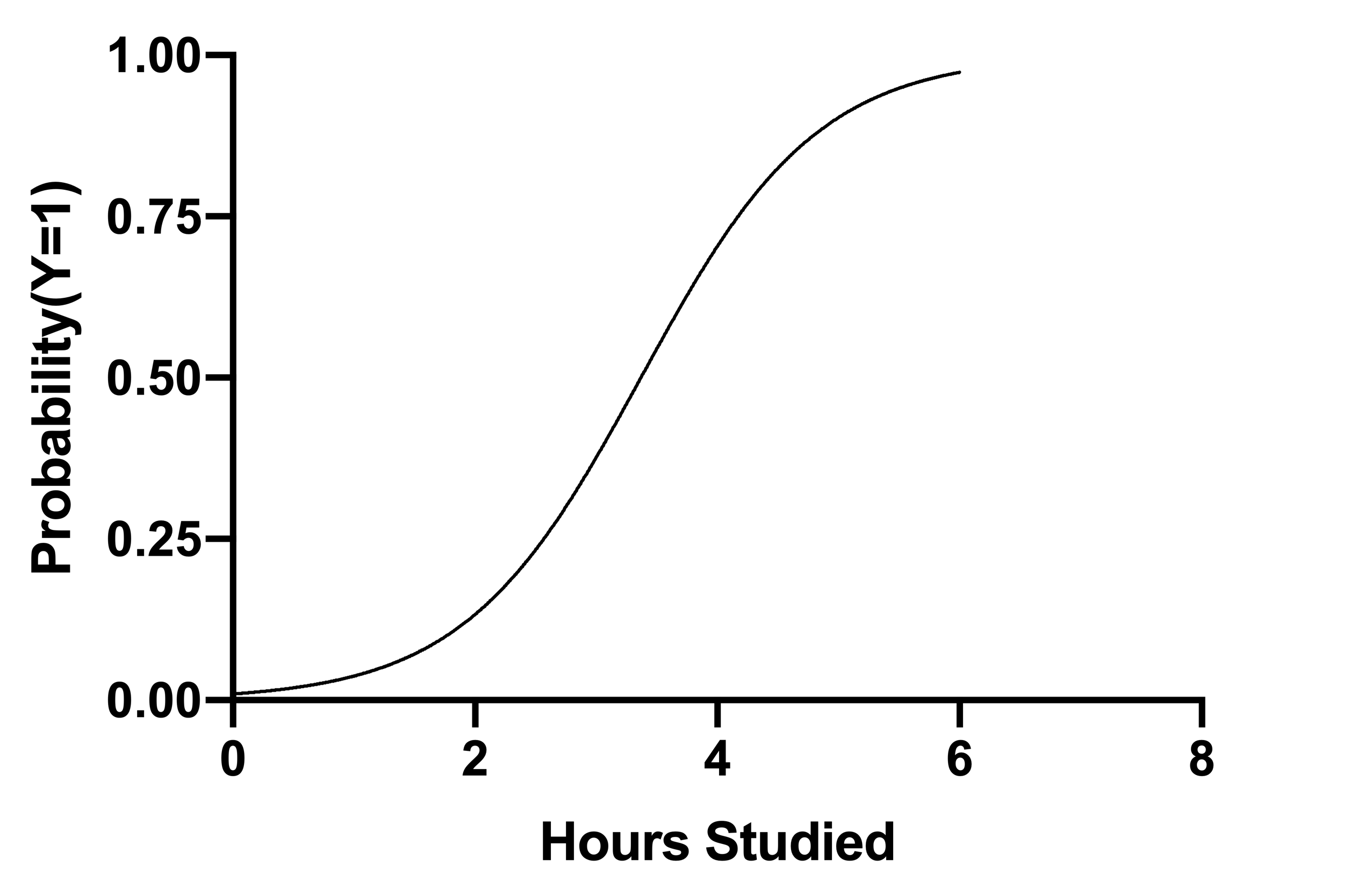
关于所有这些不同的变换，还有最后一点需要考虑。虽然简单逻辑回归的图形一般是概率与 X 的 S 型逻辑曲线，但也可以用上面的数学方法绘制几率与 X 的对数曲线。下图展示了这一点：

[概率 Y = 1] vs. X

β0 = -4.614, β1 = 1.370

对数（几率） vs. X

β0 = -4.614, β1 = 1.370