隐式方程是 Y 出现在等号两边的方程。Prism 将(尝试)根据您的数据拟合隐式方程定义的模型。
隐式方程本示例
遵循质量作用定律的结合位点平衡时的总结合模型为
Y = NS*X + Bmax*X/(Kd + X)
该模型假定 X 是配体的自由浓度。由于 X 实际上是您输入的浓度,该模型假定只有极少部分配体与之结合,因此即使 X 是您输入的浓度,也非常接近自由浓度。
如果有相当一部分配体结合了呢?Prism 中内置了一个复杂得多的模型来处理这种情况。但在其他类似情况下,可能还没有推导出模型,而且推导模型可能非常困难甚至不可能。隐式方程来救场。
在上述情况下,很容易写出隐式方程。模型中有三个地方会出现 X。您输入的 X 值是配体的总浓度。进入模型的值必须是游离浓度,即总浓度减去结合的浓度。假设 X 和 Y 的单位相同,我们只需在所有三个地方用 X-Y 代替 X 即可:
Y = NS*(X-Y) + Bmax*(X-Y)/(Kd + (X-Y))
在实际拟合数据时,您可能需要对方程稍作改动(如下所示),以处理单位转换,从而以 nM 而不是 cpm 报告 Kd。
如何用 Prism 拟合隐式方程
在 "方程 "对话框顶部选择隐式方程类型,然后在等号两边定义 Y 的方程。
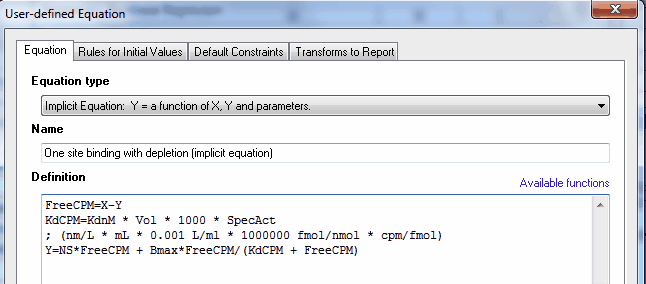
就是这样。与其他用户定义的方程一样,您需要定义约束条件和初始值。
注意事项
•在本示例中,你实际上看不到 Y 在同一方程行的等号两边。但第一行将 Y 放在等号的右侧,第四行将其放在等号的右侧。这就使得方程隐式化了。
•如果像本示例中那样从 X 减去 Y,那么 X 和 Y 必须使用相同的单位。这里输入的都是每分钟放射性计数(cpm)。当然,如果 Y 单位是 cpm,而 X 单位是 nM,那么从 X 中减去 Y 就没有意义了。
•Prism 发现隐式方程比普通方程更难拟合。您可能需要在初始值和约束条件上做文章,才能使其正常工作。计算所需时间更长,不过在数据集较小和计算机速度较快的情况下可能并不明显。
•在显式方程中,Y 出现在等号的两边,而 X 必须只出现在等号的右边。
•在本示例中,显式方程已经推导出来,甚至已经内置到 Prism 中。您可以下载的文件(链接如下)以两种方式(显式方程和隐式方程)拟合数据,结果完全相同。在其他情况下,可能很难或无法导出显式方程。