引言

当散点是由许多独立且加权因子的总和造成时，数据服从高斯分布。

根据高斯数据绘制的频率分布（直方图）看起来就像钟形高斯分布。

步骤

您拟合的数据必须是 XY 表上的频率分布形式。X 值是分区中心，Y 值是观察值的数量。

如果从一列数据集开始，使用 Prism创建频率分布，请确保将图形类型设置为 "XY 图形"，并设置点或直方图尖峰。这样，Prism 就能创建一个 XY 结果表，并将二进制中心作为 X 值输入。如果选择条形图，Prism 会创建一个列结果表，并根据分区中心创建行标签。这种表格不能用非线性回归拟合，因为它没有 X 值。

从频率分布表开始，点击分析，从 XY 分析列表中选择非线性回归，然后从 "高斯"方程组中选择 "高斯"方程。

模型（高斯分布）

Y=Amplitude*exp(-0.5*((X-Mean)/SD)^2)

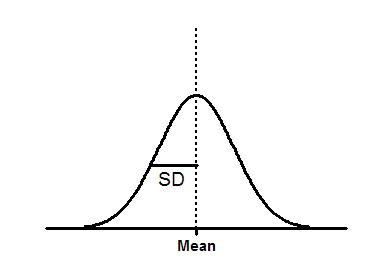
振幅是以 Y 为单位的分布中心高度。

平均值是分布中心的 X 值。

标差是对分布宽度的测量，单位与 X 相同。

平均值和标差与直接从原始数据计算出的平均值和标差不尽相同。造成差异的原因有两个。首先，创建频率分布需要对箱宽进行相当任意的决策，这将影响均值和 SD 的拟合优度值。第二个原因是，非线性回归假设残差（点与曲线的距离）服从高斯分布。这个假设在频率分布中不会完全正确。

模型（两个高斯分布之和）

如果您的数据是从两个高斯分布中采样的值的混合物，则将频率分布拟合到两个高斯分布之和的模型中。

One=Amplitude1*exp(-0.5*((X-Mean1)/SD1)^2)

Two=Amplitude2*exp(-0.5*((X-Mean2)/SD2)^2)

Y= 一 + 二

 

振幅 1 和 振幅 2 是以 Y 为单位的分布中心高度。

平均值 1 和 平均值 2是两个分布中心的 X 值。

SD1 和 SD2是两个分布的宽度，单位与 X 相同。

Prism 在为参数分配初始值方面并不十分智能。如果在拟合模型时遇到困难，可以尝试调整参数初始值。

高斯分布下的面积

高斯分布下的面积等于振幅*SD/0.3989。这个常数等于两个圆周率平方根的倒数。