当 X 值是剂量或浓度的对数时，使用该方程。当 X 值为浓度或剂量时，使用相关方程。

引言

有些药物可能在低浓度时产生抑制反应，而在高浓度时产生刺激反应，反之亦然。最终的结果是呈钟形的剂量反应曲线。

这里解释的模型是两条剂量反应曲线的总和：一条是刺激曲线，一条是抑制曲线。要精确确定所有参数，需要大量的数据点。由于这一要求，尝试拟合这类模型往往会得出"不稳定"的拟合优度参数值。在这种情况下，拟合结果可能无法提供您所需的分析见解，但作为绘制数据平滑曲线的一种方法，该模型可能仍然有用。

具体步骤

创建 XY 数据表。在 X 中输入激动剂浓度的对数，在 Y 中以任何方便的单位输入反应。

在数据表中点击分析，选择非线性回归，然后选择方程面板： 剂量-反应-特殊，X 为对数（浓度）。然后选择钟形剂量反应，X 为对数（浓度）。

考虑将 nH1 和 nH2 限定为 1.0（刺激）和-1（抑制）的恒定值。

模型

Span1=Plateau1-Dip

跨度2=高原2-陡坡

Section1=Span1/(1+10^((LogEC50_1-X)*nH1))

Section2=Span2/(1+10^((X-LogEC50_2)*nH2))

Y= Dip+Section1+Section2

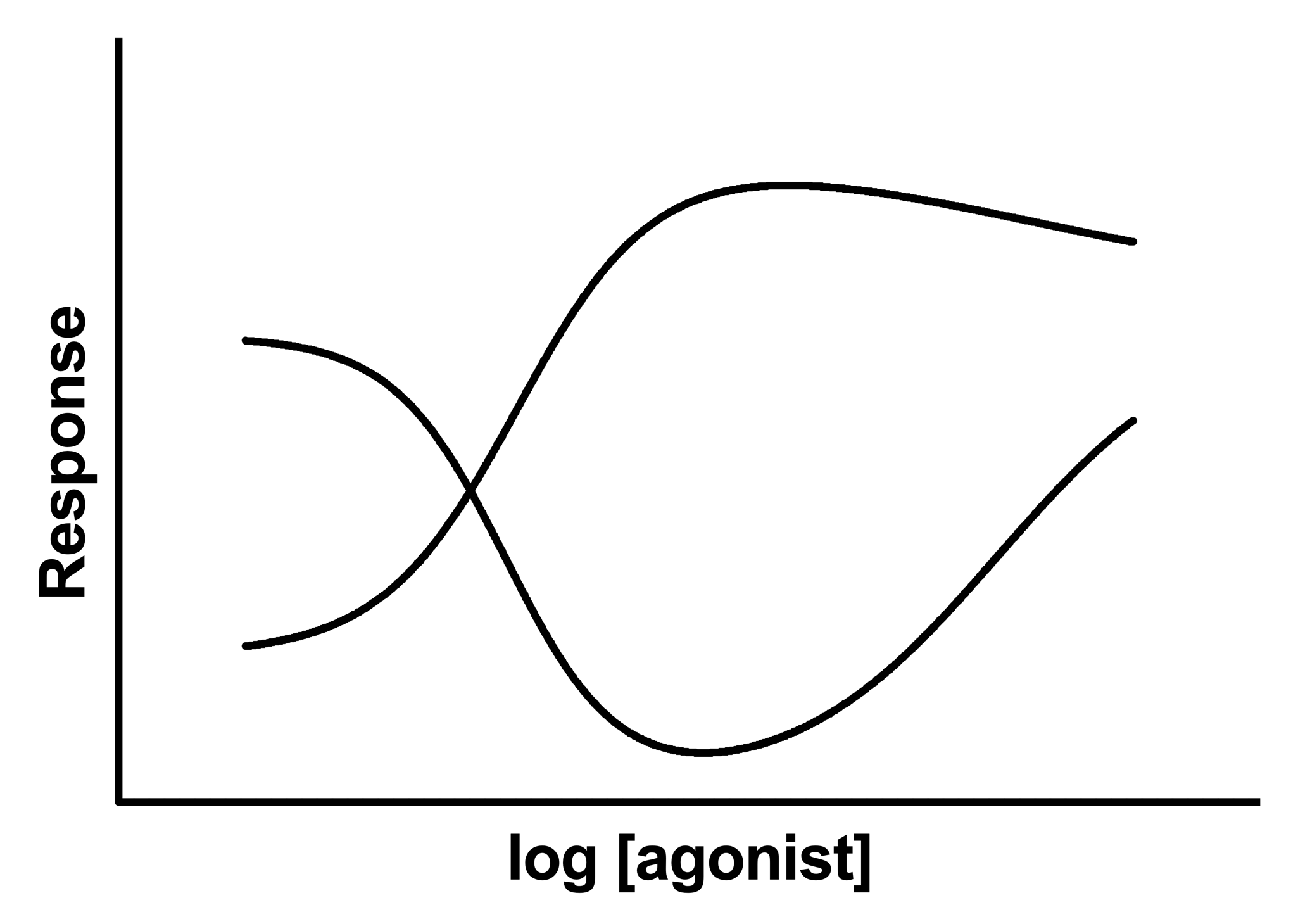
解读参数

Plateau1和Plateau2是曲线左右两端的高原，单位与 Y 相同。

请注意，当曲线先上升（后下降）时，名为 "Dip"的参数最好命名为 "Peak"。

LogEC50_1和LogEC50_2是产生半最大刺激和抑制作用的浓度，单位与 X 相同。

nH1和nH2是无单位的斜率因子或 Hill 斜坡。考虑将其限制为等于 1.0（刺激）和-1（抑制）。