引言
根据三元复合物模型,拟合别构调节剂结合的 "竞争性"曲线。请注意,该模型假定别构调节剂过量存在,因此不会因与受体结合而耗竭。由于它与放射性配体结合的位点不同,因此 "竞争性"一词并不恰当,但我们在此列出它,因为实验设计与竞争性结合所用的相同。
步骤
创建 XY 数据表。在 X 中输入未标记调节剂浓度的对数(以 nM 为单位),在 Y 中输入特异性结合,单位不限。
在数据表中点击分析,选择非线性回归,选择竞争性结合方程面板,然后选择别构调节剂滴定。
您必须根据实验设计将两个参数限制为常数:
•RadioligandNM 是标记配体的浓度,单位为 nM。整个实验使用单一浓度的放射性配体。
•HotKdNM 是标记配体的平衡解离常数,单位为 nM。
还可以考虑将 Y0(在没有调节剂的情况下放射性配体的结合)限制为一个恒定值。
模型
AlloNM=10^(X+9)
KbNM=10^(logKb +9)
alpha=10^logAlpha
KAppNM=HotKDnm*(((1+(AlloNM/KBNM))/(1+alpha*(AlloNM/KBNM))))
HotOccupancy = RadioligandNM/(RadioligandNM + HotKDnm)
Y=(Y0/HotOccupancy)*(RadioligandNM/(RadioligandNM + KAppNM))
解读参数
Kb是调节剂结合的平衡解离常数(摩尔)。
Alpha 是三元复合物常数。当 alpha=1.0 时,调节剂不会改变结合。如果 alpha 小于 1.0,则调节剂会减少配体的结合。如果 alpha 大于 1.0,则调节剂会增加结合力。
Y0是没有调节剂时放射性配体的结合力。可以考虑将其限制为一个恒定值。
注意事项
该模型旨在分析未标记化合物通过别构位点起作用时的数据。由于标记配体和未标记配体是通过不同的位点起作用的,因此将这类实验称为 "竞争性结合实验"是不恰当的(也是不正确的)。事实上,在某些情况下,别构调节剂会增强放射性配体的结合。
编写模型是为了拟合 alpha 的对数,而不是 alpha 本身。这是因为 alpha 是不对称的(所有从 0 到 1 的值都意味着调节剂会降低结合力,而所有从 1 到无穷大的值都意味着调节剂会增强结合力。在对数标度上,其值更加对称,因此按对数标度计算的置信区间(如 Prism 所做)更加准确。
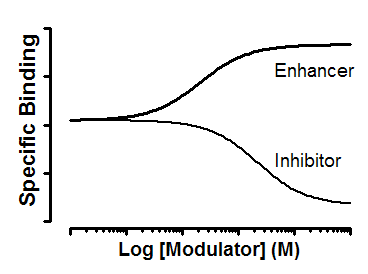
Y 轴绘制的是特异性结合。即使在抑制剂浓度非常高的情况下,特异性结合也不会降为零。这就是异位抑制的本质。如果 alpha 非常高,那么结合力几乎被抑制为零。如果 alpha 值不高,那么最大抑制作用就比较温和。本示例中,如果α=3,则最大抑制率降至 33%。
该模型假定别构调节剂过量存在,因此您添加的浓度与其游离浓度非常接近。当别构调节剂的浓度受到限制时(如 G 蛋白改变激动剂与许多受体的结合时),该模型就不适用了。任何显式模型都无法处理这种情况。您需要用隐式方程(Y 在等号两边)来定义模型,而 Prism 无法处理此类方程。
参考资料
A.Christopoulos and T. Kenakin, Pharmacol Rev, 54: 323-374, 2002