解读 Prism 同时拟合斜率和截距时的 P 值
Prism 报告了检验总体斜率为零这一零假设的 P 值。P 值回答了这个问题:
如果 X 和 Y 之间总体上不存在线性关系,那么随机选取的点导致回归线与水平线相差(或更远)的概率是多少?
同理:
如果 X 和 Y 之间总体上没有线性关系,那么随机选取的点导致R2值与您观察值一样高(或更远)的概率是多少?
P 值由 F 检验值计算得出,Prism 还会报告 F 值及其自由度。通过斜率除以标准误差计算出的 t 比值也能得到精确的 P 值。
解读 Prism 只拟合斜率时的 P 值
当您强迫直线通过原点或其他点时,要小心线性回归的 P 值。这很容易造成误解。下图说明了这个问题:
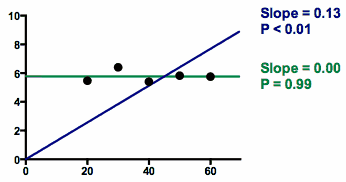
数据点几乎形成一条水平线。
用线性回归的通常方法拟合时(同时拟合斜率和截距;绿线),斜率的最佳拟合值为 0.00。P 值回答了问题:如果真实斜率为零,那么仅由于随机抽样,斜率比观察到的斜率离零更远的概率是多少。由于观察到的斜率为零,因此获得比观察到的斜率离零更远的斜率的几率几乎为 100%!因此,P 值大于 0.99,这是 P 值所能达到的最高值。有些人感到困惑,他们认为 P 值应该很小,纯粹是因为这些点有规律可循。其实不然。从传统的线性回归拟合斜率和截距来看,只有当点形成非水平的线性模式时,P 值才会小。
如果线性回归拟合的约束条件是直线必须通过原点(蓝线),那么结果就会截然不同。为了使直线既通过原点,又靠近点,拟合优度线的斜率远离零。由于直线远离水平线,所以 P 值很小。考虑到直线必须经过原点(X=0,Y=0;图的左下方)这一约束条件,拟合优度线远离水平线的数据很有说服力,因此 P 值很小也就在情理之中了。
限制直线通过原点(或其他点)在某些情况下非常有用。通常这个选项用于拟合用于插值的校准曲线,在这种情况下 P 值就没有什么用处了。如果强制直线通过原点,那么在解读 P 值时要非常小心。它很少有用,而且容易误解。