绘制残差图并进行正态性检验

残差是 Y 的实际值与预测值之间的差值。Prism 7 可以绘制一种回归的残差图。

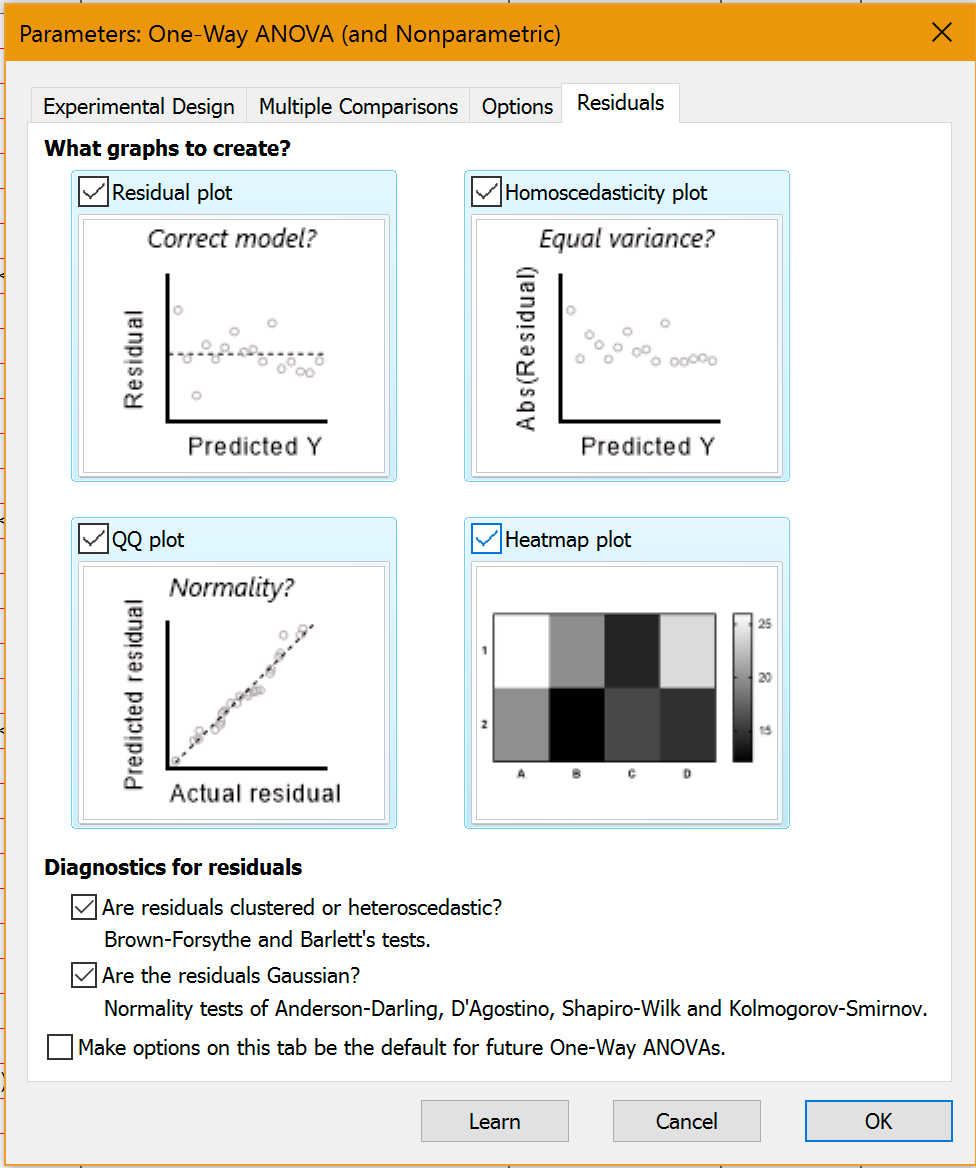
Prism 8 扩展了这一功能，还可以将单向、双向或三向方差分析、t 检验和多元回归的残差绘制成表格。对于每一种分析，用四种方法检验残差的正态性，并用四种方法绘制残差图（包括 QQ 图）。

 

泊松回归

当 Y 值代表对象或事件的实际计数数（未以任何方式归一化）时，期望残差不服从高斯分布，而是服从泊松分布。

Prism 现在，您可以在非线性回归和多元回归中指定预期的泊松回归残差，并据此进行计算。

 

逻辑回归

当结果变量（Y 值）为二元变量（是/否、1/0、生/死等）时，可以使用逻辑回归来拟合数据模型。Prism 8.3.0 的新功能是，您现在可以使用单个预测因子变量（X 变量）执行简单逻辑回归，也可以使用多个预测因子变量执行多重逻辑回归。

 

更多用于非线性回归的内置方程

•Pade(1,1)近似方程，当标准曲线在大浓度下出现高原时，可用于插入值（它类似于直角双曲线）。

•生长方程族。这些方程用于从培养细胞数量增长到经济增长的所有方面。提供的方程有指数增长方程、指数高原方程、Gompertz 增长方程、逻辑增长方程和 beta 增长方程（先增长后衰减）。

•用于模拟细胞受辐射后死亡的 线性-二次模型的几种形式。

•合页函数。它与分段线性回归相同，不同之处在于两条直线的连接是一条平缓的曲线，而不是一个硬角。

•将直线拟合到两个数据集，并找出交点和两个斜率。

•在Prism 8.2 中，我们扩展了方程库，现在所有剂量反应方程都有 X 代表浓度和 X 代表对数（浓度）时的形式。

 

不对称（剖面似然）置信区间

•计算不对称剖面似然置信区间的速度要快 2-3 倍。

•对于困难方程，Prism 有时会报告"???"，而不是一个或两个置信区间的值。这种情况仍有可能发生，但频率要低得多。

新选择

•在非线性回归中选择删除异常值时，现在可以要求Prism 用 "干净 "数据（不含异常值）创建结果表。

•检测非线性回归中的 "不稳定 "参数：Prism 8.2 中引入的新功能 "Prism Labs"，可替代Prism 用来检测不良拟合的方法。早期版本检测的是 "模糊拟合"。通过可选设置（在非线性回归的 "置信度 "选项卡上），Prism 可检测 "不稳定 "参数。根据我们的经验，这种方法更好，因为 "模糊 "方法有时无法显示新方法可以显示的结果。