在Prism 以前的所有版本中，非线性回归拟合参数的置信区间总是围绕拟合优度值对称的。这些区间被称为 渐近 区间或近似区间。这也是大多数非线性回归程序的报告内容。但在很多情况下，参数值的真正不确定性是不对称的。在这种情况下，对称置信区间并不能很好地表达参数估计的精度。

Prism 7 可以让你选择创建不对称置信区间。根据计算这些区间所使用的方法，它们有时也被称为 剖面似然区间。这些区间几乎总能更好地表达参数估计的精度，有时甚至更好。

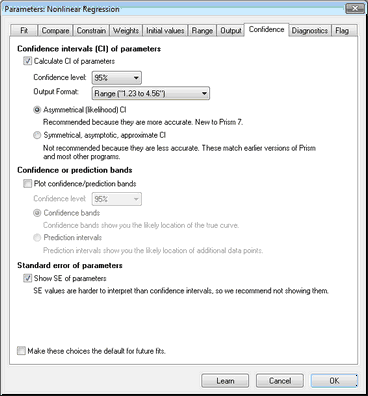
初始默认值是显示不对称区间，但可以更改默认值（在非线性回归对话框的置信区间选项卡中）。由于参数标准误差的唯一目的是计算近似置信区间，我们建议您在习惯了新的不对称区间后就不再显示这些区间。

这种计算置信区间的新方法的唯一缺点是计算速度较慢。但是，如果数据集不大（几十个数据点），采用标准模型，计算机速度也相当快，你就不会注意到这一点。 Prism 7 计算非线性回归的速度比以前的版本更快（如果选择内置方程，大约快十倍），所以你不太可能注意到计算速度变慢了。

有了这些新的不对称置信区间，我们就可以添加 新的剂量反应方程 ，其中 X 是剂量或浓度，而不是剂量或浓度的对数。