在进行等效性测试之前，首先必须确定一个治疗效果的范围，您认为这个范围在科学或临床上是微不足道的。您必须根据科学或临床判断来设定这个范围 -- 统计分析帮不上忙。

如果你观察到的治疗效果不在这个科学或临床上微不足道的范围内，那么显然你就不能断定这两种治疗方法是等效的。

如果治疗效果确实在临床或科学判断范围之内，那么你就可以问数据是否足够严密，从而得出治疗等效的有力结论。

用置信区间检验等效性。

下图显示了如何用置信区间检验等效性的逻辑。横轴表示治疗效果的绝对值（平均反应之间的差异）。填充的圆圈表示观察到的效果，即在无差异区内。横向误差条显示单侧置信区间 95%，表示与数据一致的最大处理效果（置信区间 95%）。

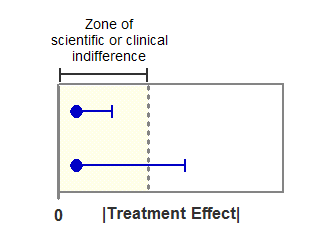
在上面显示的实验中，即使置信区间的极限也位于无差异区内。您可以得出结论（置信度为 95%），两种处理方法是等效的。

在下图所示的实验中，置信区间超出了无差异区。因此，您不能得出两种治疗方法等效的结论。你也不能得出结论说这两种处理不等效，因为观察到的处理在无差异区内。对于这样的数据，你根本无法得出等效的结论。

使用统计假设检验来检验等效性

用置信区间（上文）来思考统计等效性是非常简单的。将统计假设检验的思想应用于等价性则要棘手得多。

统计检验从零假设开始，然后询问是否有足够的证据来拒绝该零假设。在寻找差异时，零假设是没有差异。在等效测试中，我们要寻找两种治疗方法等效的证据。因此，在这种情况下，"零"假设是两种治疗方法并不等同，而是差异仅勉强大到不属于科学或临床不重视的范围。

在上图中，将零假设定义为真实效果等于虚线表示的效果。然后问：如果该零假设为真，那么（考虑到样本量和变异性）观察到与观察到的一样小或更小的效应的几率是多少。如果 P 值很小，则拒绝非等效的零假设，因此得出治疗等效的结论。如果 P 值很大，则数据符合非等效的零假设。

由于您只关心获得比零假设低这么多的效果的几率（如果差异更大，您就不会做检验了），所以您使用单尾 P 值。

上图的横轴是效应的绝对值。如果绘制治疗效果图本身，就会出现两条围绕 0 点对称的虚线，一条显示治疗效果为正，另一条显示治疗效果为负。这样就会有两个不同的零假设，每个假设都要进行单尾检验。这就是所谓的 "两个单边检验程序"（1, 2）。

两种方法是等效的

当然，使用 95% 置信区间法（使用单侧置信区间 95%）和假设检验法（使用单侧 0.05 显著性阈值）是完全等价的，所以总是给出相同的结论。在我看来，置信区间的理解要直接得多。

用 Prism 检验等价性

Prism 没有任何内置的等效性检验。但您可以使用 Prism 进行计算：

1.用 t 检验（配对或非配对组，依赖度取决于实验设计）比较两组。

2.选中创建90%置信区间的选项。没错是 90%，而不是 95%。

3.如果90%置信区间的整个范围都在你定义的无差异区内，那么你就可以以95% 的置信度得出结论：两种处理方法是等效的。

参考文献

1.D.J. Schuirmann, A comparison of the Two One-Sided Tests Procedure and the Power Approach for assessing the equivalence of average bioavailability, J. Pharmacokinetics and pharmacodynamics, 115: 1567, 1987.

2.S. Wellek, Testing Statistical Hypotheses of Equivalence, Chapman and Hall/CRCm, 2010, ISBN: 978-1439808184.