主成分回归（PCR）是 PCA 和多元线性回归（MLR）的结合。通常，通过 PCA 进行降维的目的就是 PCR，Prism 提供了执行 PCR 的功能，作为 PCA 选项的一部分。如果选择将 PCR 作为 PCA 的一部分来执行，那么 PCA 结果除了包含 PCA 的其他结果外，还将包含一个额外的回归结果选项卡。

简而言之，运行 PCA，选择一定数量的主成分，然后使用这些选定的 PC 分数作为自变量（预测因子）变量运行 MLR。 另一个由您选择的变量（不包括在 PCA 中）是因变量（结果）。

Prism 在幕后还做了另一个步骤。它不是按照 PC 分数的比例报告回归系数，而是将回归系数变回原始输入变量的比例。

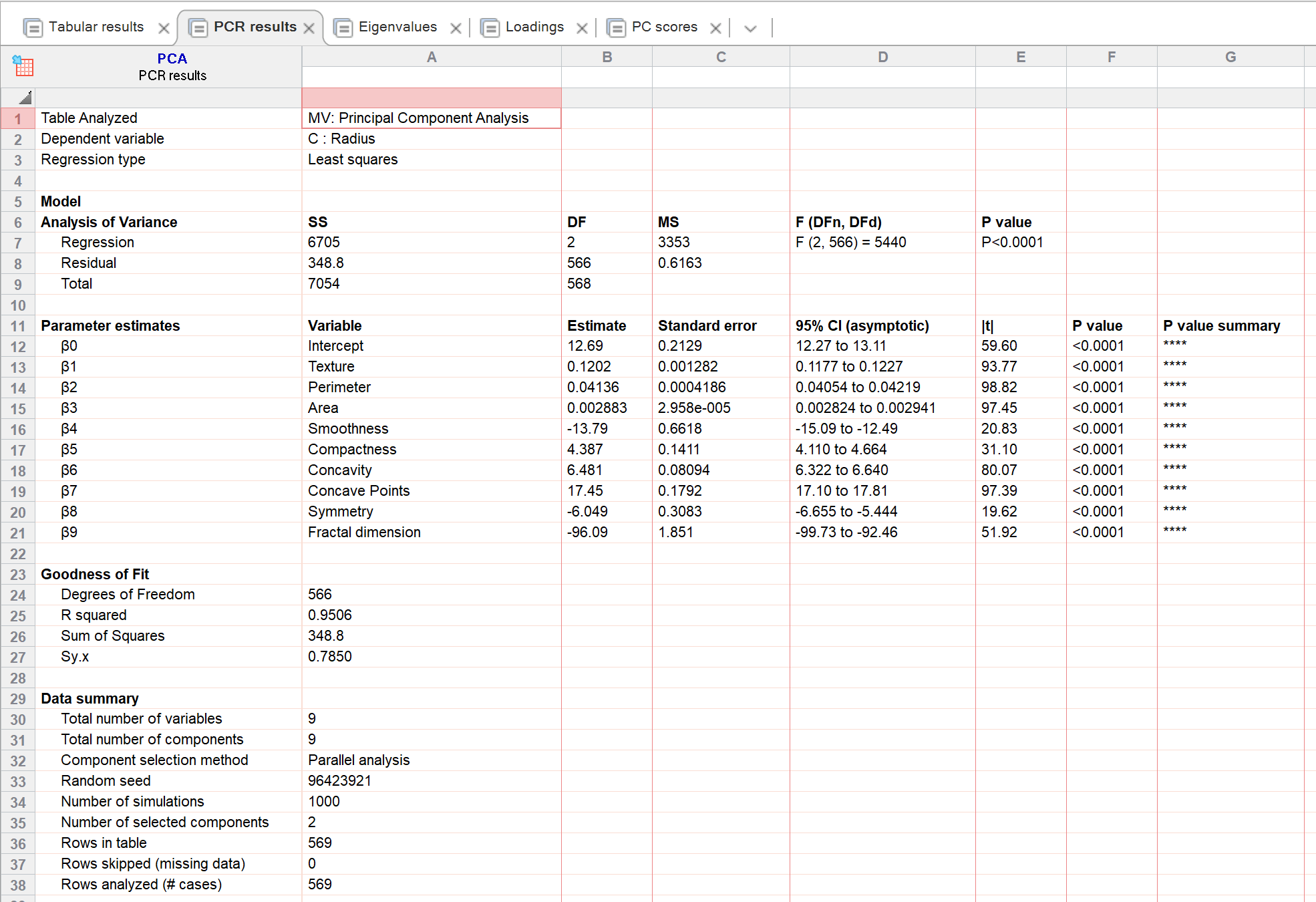
请注意，在下面显示的 PCR 结果中，回归模型使用了两个自由度，因为只选择了两个 PC 作为独立变量。 但请注意，显示的是所有九个自变量加上截距的系数。这似乎令人费解，但这正是 PCR 的意义所在。从本质上讲，MLR 是对投射到较少维度的数据进行拟合（这听起来可能很花哨，在这里有更详细的解释）。

除了使用 PC 分数拟合 MLR 外，对系数、标准误差和置信区间的解读与 MLR 相同。本示例中的模型为

估计响应 = β0+β1*X1+β2*X2+β3*X3+ ...

请查阅这些多元线性回归的附加页面，了解如何解读方差分析表、P 值和R2。

主成分是 PCR 的预测因子，而不是原始变量

有一点需要注意。首先，我们把数据点（数据表中的完整行）的总数称为 "N"。此外，我们把所选 PC（预测因子变量）的数量称为 "k"。

方差分析表中的总自由度定义为 N-1。为什么要减去 1？因为截距是拟合的。回归的自由度定义为等于 k，残差的自由度定义为 N-k-1。简单核对一下就知道，回归的自由度加上自由度等于自由度总数：

dfreg+dfres= k + (N-k-1) = N - 1 =dftotal

在拟合优度部分，自由度定义为分析行总数（N）减去参数数。参数个数不同于预测因子个数，因为该模型包含一个截距项。这意味着参数总数等于预测因子数加 1，即 k+1。因此，为了计算拟合优度部分的自由度，我们最终得出了

dfgof= N - (k+1) = N - k - 1

上面的本示例有 569 行数据，结果表显示了 10 个参数（9 个预测因子加上截距）的参数估计。然而，回归只有 2 个自由度，残差则有 566 个自由度。这是因为回归实际上只 "看到 "两个主成分作为预测因子（或自变量）。因此，自由度的计算结果为 569 - 3 = 566（3，因为它拟合了两个主成分加上截距）。这就是 PCR 的 "神奇 "之处。PCA 过程将自变量的数量减少到较少的主成分数量（不会丢失太多信息），因此 "赋予 "了分析更多的自由度。

PCR 的数据汇总

与 PCA 表格式结果的数据摘要一样，PCR 结果也包括数据摘要部分。在这一部分中，提供了与原始变量数量、PC 选择方法、所选成分数量（用作 PCR 的预测因子）以及数据表中的数据行有关的信息。虽然 PCA 和 PCR 的数据摘要中的这些值都是相同的，但需要注意的是，PCR 最后两行中跳过的行数（缺失值）和分析的行数（案例数）可能与 PCA 不同。

回顾一下，为了执行 PCR，必须从输入数据表中选择一个变量作为回归的依赖度（结果） 变量，而且该变量不能作为 PCA 的变量。然后，对选定的变量进行 PCA。如果这些变量中存在任何变异性缺失值（或排除值），则在 PCA 计算过程中将跳过这些行。然后，使用计算出的 PC 和指定的响应（结果、依赖度）变量执行 PCR。对于 PCR，Prism 会检查定义 PCs 的变量或响应变量中是否有缺失（或排除）值，而跳过在这些变 量中有缺失值的行。

为了确保这一点非常清楚，我们可以从另一个角度来考虑。PCA 中生成的成分是使用指定输入变量（不包括因变量）中所有可能的数据定义的。然后将这些成分与指定的依赖度变量进行回归。如果某行缺失一个因变量值，该行就会被排除在回归之外，但该行的其他值仍会在确定主成分值时发挥作用。

总之：

•在 PCA 中因缺失（或排除）值而跳过的行，在对同一数据进行 PCR 时也会被排除在外

•在指定响应变量中缺失（或排除）值的行将仅 在 PCR 中被排除。如果某行只缺失响应变量的值，但所有其他输入变量都有值，则该行将用于 PCA，但在 PCR中将被跳过。

•因此，对于相同的数据，PCR 的 "跳过行数（缺失数据）"有可能高于 PCA 的 "跳过行数（缺失数据）"。