随机还是伪随机？

生成真正随机数的唯一方法是通过随机物理过程，例如掷骰子或测量放射性衰变之间的间隔。Prism 和所有计算机程序一样，通过定义的计算生成"随机"数字。由于数字序列是可重复的，数学家们称其为"伪随机"数字。

真正的随机数和伪随机数之间的区别很少造成问题。在大多数情况下，计算机生成的随机数的随机性足以模拟数据和测试分析方法。

Prism 在计算第一个随机数时会使用一天中的时间，因此每次运行程序都会得到一系列不同的随机数。

来自高斯分布的随机数

Prism 使用改编自《Numerical Recipesin C》（W. H. Press et al，第二版，剑桥出版社，1992 年）一书的例程，从高斯分布中生成随机数。函数 RAN3（定义在 Numerical Recipes 中）生成均匀分布的随机数，函数 GASDEV 将其转换为均值为零且标准偏差由您输入的高斯分布。

如果选择相对误差，Prism 会首先从均值为零、标准差等于输入误差百分比的高斯分布中计算出一个随机数。然后将该百分比乘以理想的 Y 值，得出实际随机值，并将其添加到 Y 值中。

来自 t 分布的随机数

Prism 还可以生成任意自由度（df）的 t 分布随机数。这样就可以模拟比高斯分布更广泛的散度。如果 df 较小，则分布非常宽。如果 df 较高（超过 20 左右），则与高斯分布几乎没有区别。如果 df=1，则分布极宽（异常值很多），与洛伦兹分布（也称为柯西分布）相同。Prism 使用此公式从自由度为 df 的 t 分布中生成随机数：

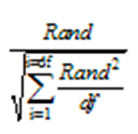
要从具有 df 自由度的 t 分布中计算随机数，Prism 会从高斯分布中生成 df+1 个不同的随机数。

泊松或二项分布的随机数

我们从 WH Press 及其同事所著的《Numerical Recipes》第三版第 372-377 页中改编了这一思路。

请注意泊松和二项分布随机值与高斯分布随机值之间的一个重要区别。

•对于高斯随机值，模拟值等于计算出的理想值加上从高斯分布中抽取的随机误差（均值为零，标差由您指定）。我们说"加上"随机值，但这个随机值有一半时间（平均）是负值，因此模拟值有一半时间会小于理想值。

•使用泊松时，模拟值是从泊松分布中抽取的随机值，使用模拟中计算出的理想值作为泊松分布的群体值。对于高斯误差，您可以在模拟对话框中指定标准偏差。泊松误差则不同。 模拟的泊松值始终是整数。

•对于二项式，模拟值是从二项式分布中抽取的随机变量，其人口比例（或百分比）由模拟计算得出，并使用您输入的样本量。

用 Excel 计算随机数

如果您想进行 Prism 无法实现的模拟，那么 Excel 也可以实现。下面列出的方法在 Excel 2003 及更高版本中运行良好，但不应在 Excel 早期版本中使用。

Excel 提供两个随机数函数。

•RANDBETWEEN(low, high) 公式从输入的低值和高值之间（包括低值和高值）的范围内随机选择一个整数。结果始终是一个整数，因此该函数用处不大。

•RAND() 函数生成一个介于 0.0 和 1.0 之间的随机值。这是一个 Excel 函数，至少在名称上是如此，因此需要在后面加上括号，但该函数没有输入，因此括号之间没有任何内容。

如果要从高斯分布生成随机数，就需要对用 RAND() 函数生成的值进行变换。这个 Excel 公式可以从均值为 0.0、SD 为 1.0 的高斯分布中计算出一个随机数。

=normsinv(rand())

RAND() 函数计算一个从 0 到 1 的随机数。NORMSINV() 函数取 0 到 1 之间的一个分数，并告诉您需要高于或低于平均值多少个标准偏差，才能使累积高斯分布包含整个人口的该分数。

乘以标准偏差，再加上平均值，就可以得到从高斯分布中随机抽取的具有该平均值和标准偏差的数字。例如，使用本示例公式从均值为 100、标准差为 15 的高斯分布中取样：

=(NORMSINV(RAND())*15)+100